Krychle a její síť v GeoGebře 3D

Základní údaje

• Stupeň vzdělávání: 2. stupeň ZŠ, odpovídající ročník víceletého gymnázia
• Věková skupina: 12 - 14 let
• Vzdělávací obor: matematika a její aplikace
• Tematický okruh: geometrie v rovině a v prostoru
• Časová dotace:
  • Výuka: 1 vyučovací hodina
  • Příprava: 0 minut

K čemu aktivita směřuje

K vytvoření dynamického 3D modelu sítě krychle (včetně animace) jako názorné pomůcky ke správnému stanovení povrchu krychle.

Pomůcky, hardware, software

Žák/yně: PC s připojením na internet, program GeoGebra Klasik nebo aplikace GeoGebra 3D prostředí

Učitel/ka: PC s připojením na internet, program GeoGebra Klasik nebo aplikace GeoGebra 3D prostředí, dataprojektor nebo interaktivní tabule

Zdroje

GeoGebra aplikace. GeoGebra Klasik

Potřebné vstupní znalosti a dovednosti

• Oborové
  • znalost krychle
  • schopnost určit obsah čtverce z délky jeho strany
• Digitální
  • schopnost otevřít prostředí (aplikaci) GeoGebra 3D
  • způsobilost rozlišit kliknutí na levé a na pravé tlačítko myši

Přínos využití digitálních technologií

Efektivní vytvoření dynamického 3D modelu sítě krychle a její animace jako podpůrný prostředek pro rozvoj prostorové představivosti.

Metodická poznámka

Doporučujeme ovládání pomocí myši v případě práce na PC nebo dotykového pera při práci s tablety.

Článek obsahuje v příloze nápovědu pro učitele s návodem, jak otevřít 3D prostředí programu GeoGebra Klasik.

Práce ve 3D je pro operační paměť zařízení náročná. Při slabším připojení internetu může dojít k zobrazení objektu s mírnou časovou prodlevou.

Žáci si nejdříve samostatně vyzkouší jeden ze způsobů sestrojení krychle a jednoduchou manipulací s určitým vrcholem krychle změnu velikosti její hrany.

Hned v úvodu žáky upozorníme, aby nijak neotáčeli krychlí ani podstavnou rovinou, nepoužívali druhý manipulační bod (v našem případě bod C).

V úloze 1 je vhodné také se žáky vyzkoušet zobrazení hran tělesa při nastavení neprůhlednosti na hodnotu 0. Pak je ale důležité se vrátit k nastavení jiné, větší hodnoty.

V případě potřeby velikost zobrazení ve 2D nebo 3D ovládáme pomocí kolečka myši. Nastavená délka hrany krychle se nezmění.

Program zobrazí popsaným způsobem pouze jedinou síť krychle  -  tu, která má tvar latinského kříže. Na aktivity je možné navázat diskuzí se žáky o možnostech existence dalších tvarů sítě krychle.

Rozloženou síť (ve 2D) také můžeme při aktivním 2D okně přes ikonu hamburger menu (tři rovnoběžky) v pravém horním rohu postupným proklikáním výběrů Soubor – Exportovat obrázek zkopírovat, vložit například do MS Word a následně vytisknout. Aby se nezobrazil posuvník (případně osy souřadnic), provedeme jeho (jejich) skrytí (obr. 5).  Stejným způsobem lze zdokumentovat i situaci ve 3D. Musíme však mít 3D prostředí aktivní.

Žáky postupně seznamujeme i s informacemi v algebraickém okně.

Popis vzdělávací aktivity

Úloha 1 - Konstrukce krychle

1. Otevřete 3D prostředí programu GeoGebra. Zobrazí se tři okna. První, zcela vlevo, je algebraické okno, uprostřed se zobrazuje okno s nákresnou 2D a vpravo je umístěno okno grafického náhledu 3D společně se třemi souřadnými osami a rovinou, kterou budeme dále nazývat podstavná rovina (obrázek 1).
2. Sestrojte krychli o délce hrany 3 jednotky \[ (a=3~\mathrm{j}) \] užitím nástroje Krychle (umístěn v nabídce ikony s obrázkem jehlanu v grafickém náhledu 3D) tak, že kliknete nejdříve na společný průsečík všech tří os a pak na bod 3 na ose \[ x \].
3. Poloha kurzoru je v okně 3D náhledu. Přes pravé tlačítko myši skryjte osy.
4. Přesuňte kurzor do řádku algebraického okna s označením krychle. Opět pomocí pravého tlačítka myši aktivujte Nastavení a v něm změňte barvu tělesa na černou a nastavte neprůhlednost blíž k nule, obr. 2. (Pozor, nikdy nenastavujeme polohu 0, znemožnili bychom tak správné rozlišení viditelných a neviditelných hran v zobrazení tělesa.)
5. V nákresně 2D uchopte první manipulační bod (v našem případě označen B ) a tažením měňte délku hrany krychle. Sledujte, jak se mění velikost tělesa v grafickém náhledu 3D.
6. Nastavte polohu manipulačního bodu B tak, aby se ve 3D zobrazila opět krychle s délkou hrany \[ a=3~\mathrm{j} \].

    

Řešení

Úloha 2 - Síť krychle 

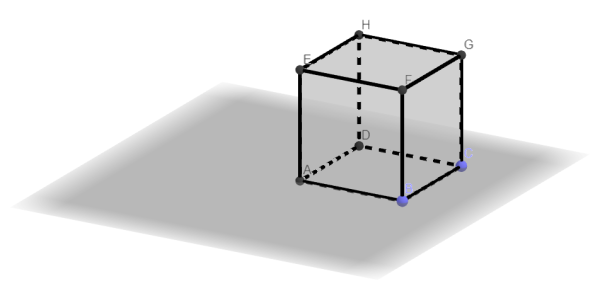
Pracujeme s modelem krychle o délce hrany \[ a=3~\mathrm{j} \], kterou máme připravenou z úlohy 1. Vytvoříme si dynamický model sítě krychle.

1. Klikněte kamkoliv do 3D náhledu. V nabídce ikony s obrázkem jehlanu vyberte předposlední Síť (obr. 3) a klikněte na těleso ve 3D náhledu. Zobrazí se dvojrozměrná síť krychle ve tvaru latinského kříže v nákresně 2D i ve 3D prostředí (obr. 4).
   

   

2. V nákresně 2D je zobrazen pohled shora (tzv. nárys) situace ve 3D prostředí. Také se zde zobrazila úsečka (v našem případě pojmenována b) s vyznačeným bodem (černý puntík). Jedná se o tzv. posuvník, s jehož pomocí síť rozpohybujeme. Stisknutím levého tlačítka myši „uchopte“ vyznačený puntík, držte a pomalu jím pohybujte po úsečce. Rozložená síť zmizí z nákresny 2D, ale v grafickém náhledu 3D můžeme pozorovat, jak se síť složí do původní krychle a jak se síť krychle rozloží do roviny. Síť vidíme ve 2D nákresně pouze v případě, kdy je ve 3D okně rozložena do podstavné roviny.

   

3. Umístěte kurzor na úsečku b v nákresně 2D a přes pravé tlačítko myši aktivujte animaci. Skládání a rozkládání sítě se provádí samo. Animaci zastavíte kliknutím na bod (puntík) na úsečce b.
4. Popište, z čeho se skládá síť krychle. Jaký obsah mají všechny tyto mnohoúhelníky – celá síť?

Řešení

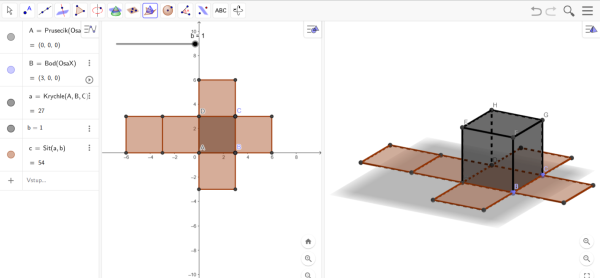
Výsledný model prezentuje obrázek 4. 

Síť krychle (obrázek 5) tvoří šest shodných čtverců umístěných do tvaru latinského kříže. Celá síť tvoří povrch tělesa a její obsah vypočítáme jako šestinásobek obsahu každého čtverce. Platí \[ S=6\cdot9=54~\mathrm{j}^2 \]. Stejná hodnota je také zapsána v algebraickém okně v řádku s označením sítě.