Těžnice a těžiště trojúhelníku

Základní údaje

• Stupeň vzdělávání: 2. stupeň ZŠ, odpovídající ročník víceletého gymnázia
• Věková skupina: 12-14 let
• Vzdělávací obor: matematika a její aplikace
• Tematický okruh: geometrie v rovině a v prostoru
• Časová dotace:
  • Výuka: 1 vyučovací hodina
  • Příprava: 0 minut

K čemu aktivita směřuje

K vytvoření vlastního dynamického modelu a jeho využití k objevování; k aktivní aplikaci nástrojů programu na ověřování formulovaných hypotéz týkajících se vlastností těžnic a těžiště v trojúhelníku.

Pomůcky, hardware, software

• Žák/yně: PC nebo tablet s připojením na internet
• Učitel/ka: PC s připojením na internet, dataprojektor

Zdroje

Geogebra aplikace. GeoGebra Klasik 

Potřebné vstupní znalosti a dovednosti

• Oborové
  • znalost definice pojmu těžnice,
  • porozumění poměru.
• Digitální
  • ovládání základních konstrukčních nástrojů programu GeoGebra (nástroje Mnohoúhelník, Střed, Průsečík, Vzdálenost, Vztah mezi objekty).

Přínos využití digitálních technologií

Efektivní využití dynamické geometrie k modelování a ověřování vlastních hypotéz o vlastnostech těžnic a těžiště v trojúhelníku.

Metodická poznámka

Žákům je potřeba nejdříve definovat pojem těžnice.

Abychom neměli v nákresně mnoho popisků, na začátku práce se žáky společně nastavíme popisování jen nových bodů (poslední ikona vpravo nahoře, nabídka Nastavení, volba popisovat Pouze nové body, potvrdit Uložit nastavení).

V první úloze je vhodné se domluvit, které dvě těžnice sestrojíme nejdříve. Po sestrojení jejich průsečíku necháme žáky modelovat různé typy trojúhelníků a krátce diskutujeme o tom, zda společný bod může/nemůže ležet na straně trojúhelníka, v některém z jeho vrcholů, ve vnější oblasti trojúhelníku.

Třetí těžnici musíme sestrojit stejným způsobem, tj. nejdříve střed strany a poté úsečku od středu k vrcholu. Jedině tak nebude konstrukčně vázán bod T na třetí těžnici a můžeme provést ověření.

V úloze 2 musí žáci velmi pomalu pohybovat s vrcholy trojúhelníku, aby se jim podařilo nastavit přesně hodnotu 6 jednotek. Při dalším zkoumání doporučujeme, aby žáci chodili zapisovat svá zjištění na tabuli do připravené tabulky:

Zpočátku necháme žáky najít vhodná celá čísla, očekáváme, že odhalí násobky tří. Poté zkusíme ověřit platnost hypotézy pro desetinná čísla. Pozor, zde se k přesné hodnotě třetinového poměru z důvodu zaokrouhlení nemusíme vždy dostat (obě čísla musí být dělitelná třemi).

Před realizací poslední, třetí úlohy, je potřeba žákům dobře vysvětlit a také zapsat na tabuli, jakým způsobem ověření dělicího poměru provedeme. Teprve potom společně zadáme do vstupního řádku algebraického okna potřebný vzorec. V případě, že pracujeme s tablety v online prostředí, vzorec zapisujeme pomocí virtuální klávesnice programu GeoGebra, nikoli užitím klávesnice tabletu.

Podle času necháme nakonec žáky ověřit dělicí poměr i na zbývajících těžnicích.

Popis vzdělávací aktivity

Zadané úlohy řešímě se žáky společně.

Úloha 1 - Ověření společného bodu všech těžnic

1. V nákresně programu GeoGebra sestrojte užitím nástroje Mnohoúhelník obecný trojúhelník a nastavte neprůhlednost objektu na hodnotu 0 (pravé tlačítko myši, volba Nastavení, karta Barva).
2. Sestrojte dvě ze tří těžnic trojúhelníku (využijte nástroje Střed a Úsečka).
3. Najděte jejich průsečík a přejmenujte na T. (Nástroj Průsečík, pravé tlačítko myši – volba Přejmenovat).
4. Měňte polohu vrcholů trojúhelníku a sledujte odpovídající změnu polohy těžiště.
5. Sestrojte třetí, zbývající těžnici (jako spojnici středu strany a vrcholu), a změňte její barvu na červenou (pravé tlačítko myši – Nastavení, karta Barva).
6. Užitím nástroje Vztah mezi objekty ověřte, že i třetí těžnice prochází bodem T.

Řešení

Středy stran nemusíme přejmenovávat, pokud si společně stanovíme, v jakém pořadí středy budeme označovat, pak automatické pojmenování budeme mít všichni stejné (obrázek 1).

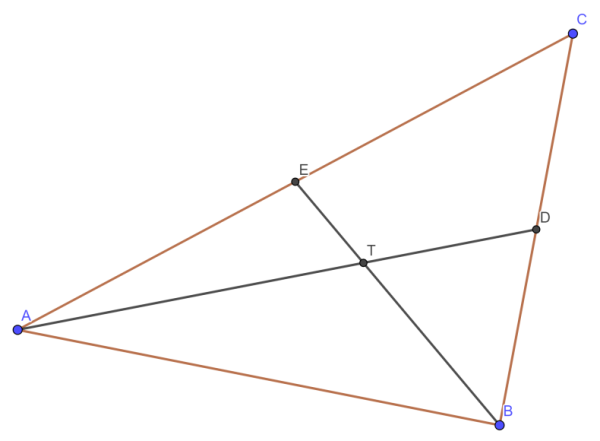
Pokud jsme dodrželi správný postup při konstrukci třetí těžnice, po použití nástroje Vztah mezi objekty se objeví informace, že bod T leží na třetí těžnici, obrázek 2. Pro lepší srozumitelnost můžeme zobrazit popis červené těžnice (pravé tlačítko myši, nabídka Zobrazit popis).

Úloha 2 - Vlastnosti těžiště trojúhelníku

1. Skryjte (nikoliv vymažte!) zobrazení prvních dvou těžnic (pravé tlačítko myši, volba Zobrazit objekt).
2. Nastavte pozici vrcholů trojúhelníku tak, aby délka červené těžnice byla 6 jednotek (hodnotu její délky sledujte v algebraickém okně).
3. Užitím nástroje Vzdálenost stanovte na červené těžnici délku úseček od vrcholu k těžišti a od těžiště ke středu strany. Zformulujte své zjištění o jednotlivých vzdálenostech.
4. Přemístěním vrcholů trojúhelníku zkuste nastavit další vhodnou délku červené těžnice. Platí i nyní vaše hypotéza?

Řešení

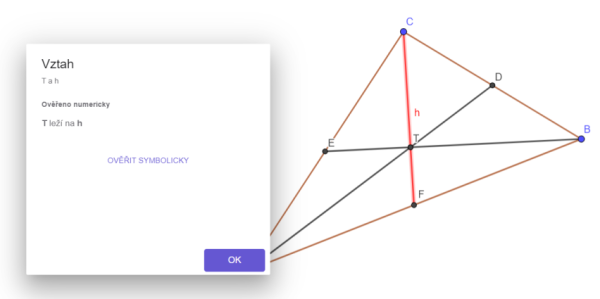
Pro těžnici o velikosti 6 jednotek jsou délky úseků zobrazeny na obrázku 3.

Úloha 3 - Ověření dělicího poměru těžiště na těžnici

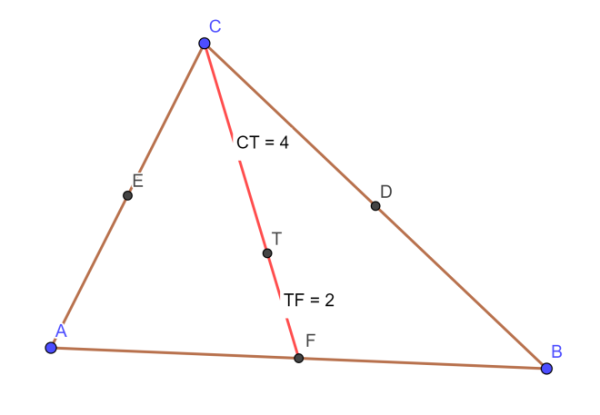
Chceme pomocí počítače ověřit, že platí vztah\[ |CT|=2\cdot|FT| \] , to znamená\[ |CT|:|FT|=2:1 \]  (podíl délek úseček je roven 2). Do vstupního řádku algebraického okna začněte psát slovo „vzdálenost“. Objeví se nabídka, ze které vyberte Vzdálenost (Bod, Objekt). Do závorek napište označení bodů a oddělte je čárkou. Pokračujte zápisem znaménka děleno a v algebraickém okně se zobrazí zlomková čára. Pro zápis jmenovatele opětovně použijte nabídku Vzdálenost (Bod, Objekt), obrázek 4.

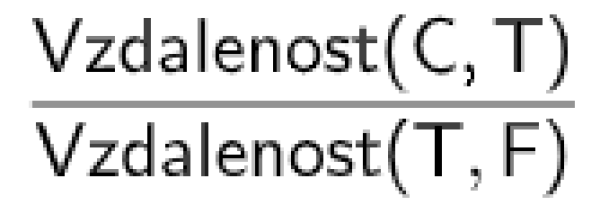
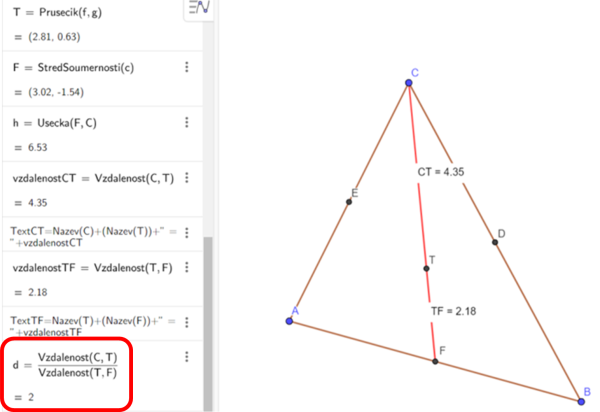
Stisknutím klávesy Enter se automaticky pojmenuje definované číslo, které je podílem dvou vzdáleností, a také se zobrazí jeho hodnota (označeno rámečkem v obrázku 5).