Statistika mzdových nákladů

Základní údaje

• Stupeň vzdělávání: gymnázium, střední škola
• Věková skupina: 15-19 let
• Vzdělávací obor: matematika a její aplikace, matematické vzdělávání
• Tematický okruh: práce s daty, statistika v praktických úlohách
• Časová dotace: 
  • Výuka: 1 vyučovací hodina
  • Příprava: 5 minut (nasdílení souboru dat žákům)

K čemu aktivita směřuje

K počítačovému zpracování známých dat - stanovení vybraných statistických charakteristik, ke schopnosti žáků správně vyhodnotit zjištěná fakta a zamyslet se nad případnými potřebnými doplňujícími informacemi.

Pomůcky, hardware, software

• Žák/yně: PC nebo tablet, MS Excel (případně obdobný tabulkový procesor)
• Učitel/ka: PC nebo tablet, MS Excel (případně obdobný tabulkový procesor), dataprojektor

Zdroje

https://csu.gov.cz/

Potřebné vstupní znalosti a dovednosti

• Oborové
  • znalost statistických pojmů: variační rozpětí, aritmetický průměr, modus, medián
• Digitální
  • základní znalost prostředí MS Excel (případně obdobného tabulkového procesoru) – zápis do buňky, přepínání karet

Přínos využití digitálních technologií

Tabulkové procesory umožňují rychlé a efektivní statistické zpracování velkého množství dat; uspořený čas lze věnovat důslednější analýze výsledků a prohlubování souvislostí statistických charakteristik.

Metodická poznámka

Vzhledem k řízené diskuzi, která je součástí aktivity, doporučujeme aktivitu realizovat v půlené hodině.

Evokaci můžeme zahájit otázkou, zda existují rozdíly (a případně jaké) ve výši měsíční hrubé mzdy pracovníků (stejného pohlaví) s nejvyšším ukončeným středoškolským vzděláním (s maturitou, bez maturity).

Každému žákovi zpřístupníme soubor s daty. Úlohu 1 řešíme pro první skupinu pracovníků společně se žáky. Údaje pro druhou skupinu pak zpracovávají samostatně, společně probíhá pouze kontrola výsledků.

Úlohu 2 zpracovávají žáci ve dvojicích a postup a řešení zapisují do sešitu. Doporučená doba na vypracování je asi 10 minut. Následně vyučující vyzve několik žáků ke slovní interpretaci zjištěných závěrů. Jedná se o řízenou diskuzi, je třeba, aby se třída shodla na společných závěrech.

Závěrečných maximálně deset minut hodiny věnujeme společné diskuzi nad řešením posledního úkolu. Je potřeba uvést, že tabulka s hrubou mzdou není bez uvedení počtu odpracovaných hodin zcela odpovídající. Můžeme žákům ukázat například grafické srovnání, případně je seznámit s dalšími charakteristikami apod.

Žáky, kteří umí dobře používat tabulkový procesor, necháme vyhotovit také grafy.

Fiktivní mzdové údaje byly stanoveny tak, aby zhruba odpovídaly stavu v roce 2024.

Popis vzdělávací aktivity

Úloha 1 - Základní charakteristiky

V souboru MS Excel jsou dvě tabulky s údaji o průměrné měsíční hrubé mzdě části zaměstnanců fiktivní firmy za sledované období. Máme před sebou finanční odměny pracovníků (mužů) s nevyšším dosaženým vzděláním SŠ bez maturity a SŠ s maturitou. Provedeme základní statistiku pro každou skupinu. S využitím nástrojů programu zjistěte následující údaje:

1. minimální a maximální hrubou mzdu, variační rozpětí mezd,
2. aritmetický průměr hrubé mzdy,
3. medián,
4. modus.

Řešení

Ke zjištění potřebných dat využijeme definované statistické funkce programu. Jejich vyvolání lze provést jedním z těchto způsobů:

1. na kartě Vzorce rozbalíme nabídku Automatického shrnutí (ikona Σ) s možnostmi Součet, Průměr, Počty, Maximum, Minimum a Další funkce;
2. na kartě Vzorce rozevřeme nabídku Další funkce a vybereme Statistické.

Statistických funkcí program obsahuje mnoho, je vhodné používat automatické dokončování vzorce. Po zadání znaku „=“ a několika počátečních písmen (psáno velkými písmeny) se zobrazí seznam platných funkcí, ze kterého vybereme tu, již potřebujeme.

Následuje podrobnější popis prvního z uvedených způsobů:

Klikneme do libovolné prázdné buňky, kde chceme mít zobrazený výsledek. Na kartě Vzorce z nabídky Automatického shrnutí vybereme funkci Minimum. Její označení MIN () se propíše do buňky (včetně nutného znaku „=“ pro zápis funkce), zbývá vložit argument funkce. Tím je sloupec číselných hodnot všech průměrných hrubých mezd v jedné tabulce. Do pozice argumentu tato data vložíme tak, že levým tlačítkem myši klikneme na buňku s první hodnotou a tahem přejedeme celý sloupec. Pokud stisknuté tlačítko pustíme, výběr buněk tak ukončíme. Potvrdíme klávesou Enter. Zobrazí se nejmenší hodnota průměrné měsíční mzdy.

Stejným způsobem zjistíme maximální hrubou měsíční mzdu. Hodnotu variačního rozpětí \[ (R=x_{max.}-x_{min.}) \] spočítáme zpaměti, případně definujeme vlastní vzorec, nejlépe s relativními odkazy na buňky.

Analogicky, jako např. při určování minimální hodnoty, využijeme z nabídky na kartě Vzorce funkci Průměr ke zjištění aritmetického průměru hodnot.

Z nabídky Automatického shrnutí můžeme také využít funkce Počet ke zjištění počtu zaměstnanců (rozsahu souboru) a Součet ke stanovení celkových mzdových nákladů.

Zbývá určit medián a modus. Nejdříve rozevřeme nabídku Další funkce, zobrazí se nové okno, do jehož prvního řádku začneme psát slovo MEDIAN. Díky automatickému dokončování vzorce nám program nabídne funkce obsahující počáteční písmeno (písmena) hledání. Vybereme MEDIAN () a označíme výběr buněk. Pro nalezení nejčastěji se vyskytující hodnoty znaku použijeme funkci MODE.SNGL(). Program vrátí hodnotu, pokud tato existuje. (Funkce MODE.MULT pak případně ukáže všechny nejčastěji se  opakující hodnoty.) V případě tabulky s průměrnou hrubou mzdou zaměstnanců bez maturity modus neexistuje, žádní dva zaměstnanci nemají stejnou průměrnou hrubou mzdu.

Zjištěné hodnoty pro každou tabulku ukazuje Obrázek 1.

Úloha 2 - Interpretace zjištěných dat

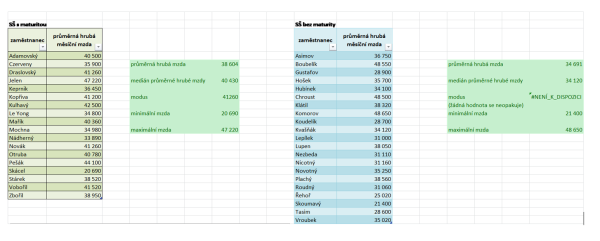
Program MS Excel už splnil svůj úkol, nyní je potřeba rozumně interpretovat zjištěné výsledky. Nejdříve vyhodnoťte každou skupinu zvlášť a pak se pokuste o porovnání obou skupin.

Řešení

1. SŠ s maturitou
   • Průměrná hrubá mzda: 38 604 Kč
   • Medián: 40 430 Kč
   • Modus: 41 260 Kč
   • Minimální mzda: 20 690 Kč
   • Maximální mzda: 47 220 Kč
   • R = 26 530 Kč
     Až na jednu - tu nejnižší - mzdu jsou ostatní v této skupině vyrovnanější. Pokud bychom ji nezapočítali, pak průměrná hrubá mzda dosáhne hodnoty 39 658 Kč (využijeme nástroj seřazení mezd od nejnižší k nejvyšší a znovu spočítáme průměr bez této hodnoty), což je údaj blízký mediánu. Je názorně vidět, jak odlehlá hodnota ovlivňuje aritmetický průměr. Dokladem může být i graf (Obrázek 2).
     
     
2. SŠ bez maturity
   • Průměrná hrubá mzda: 34 691 Kč
   • Medián: 34 120 Kč
   • Modus: neexistuje (žádná hodnota se neopakuje)
   • Minimální mzda: 21 400 Kč
   • Maximální mzda: 48 650 Kč
   • R = 27 250 Kč
     Medián je mírně nižší než průměr, což může znamenat, že několik vyšších mezd „táhne“ průměr nahoru. Jedná se o tři zaměstnance, jejichž průměrná mzda přesahuje 48 000 Kč. Kdybychom opět nezapočítali mzdy těchto zaměstnanců, průměrná mzda by dosahovala 32 379 Kč. A i vzhledem k této částce je zřejmé, že se v souboru vyskytují také odlehlé nízké hodnoty. Soubor vykazuje hodně rozptýlené hodnoty oběma směry. Můžeme opět doložit grafem (Obrázek 3).
     
     
3. Srovnání obou skupin
   Variační rozpětí je větší u pracujících bez maturity než s maturitou. Zaměstnanci s maturitou mají v průměru o cca 3 900 Kč vyšší mzdu než zaměstnanci bez maturity. Také prostřední hodnota (medián) ukazuje vyšší mzdu u maturantů (40 430 Kč vs. 34 120 Kč). Rozdíl přibližně 3 900 Kč ukazuje, že dosažení maturity má pozitivní vliv na výši mzdy. Celkově lze říci, že dosažení maturity se projevuje vyšší střední úrovní mzdy, i když nejvyšší individuální mzda se objevila u skupiny bez maturity. To ukazuje, že i bez maturity se dá dosáhnout slušné mzdy, ale většina lidí s maturitou má výdělek lepší.

Úloha 3 - Další ukazatele

Zamyslete se a zkuste navrhnout další indikátory, které by nám posloužily k lepšímu a spolehlivějšímu statistickému porovnání.

Řešení

Na prvním místě uvádíme grafické znázornění. Vizualizací, tj. vhodně vybraným grafem podpoříme správnou interpretaci statistických výsledků, jak ilustrují sloupcové grafy na obrázcích 2 a 3.

Dalšími vhodnými ukazateli jsou například charakteristiky variability: rozptyl a směrodatná odchylka, díky nimž zjistíme, jak výrazně se liší mzdy mez jednotlivci; kvartily (1. a 3.), které vyselektují zaměstnance s nejnižšími a nejvyššími příjmy.

Nelze také opomenout důležitou informaci o počtu odpracovaných hodin. Pokud někdo pracuje na plný úvazek, někdo na částečný, nelze jejich průměrné hrubé mzdy porovnávat. Může se stát, že zaměstnanec má vyšší hrubou mzdu díky množství přesčasových hodin (viz ukázka maximální mzdy ve skupině SŠ bez maturity).