Střední příčky v trojúhelníku

Základní informace

• Stupeň vzdělávání: 2. stupeň ZŠ, odpovídající ročník víceletého gymnázia
• Věková skupina: 12–14 let
• Vzdělávací obor: matematika a její aplikace
• Tematický okruh: geometrie v rovině a v prostoru
• Časová dotace:
  • Výuka: 1–2 vyučovací hodiny 
  • Příprava: 0 minut

K čemu aktivita směřuje

Žák odhalí vlastností středních příček trojúhelníku na základě experimentování, modelování a ověřování v dynamickém geometrickém programu GeoGebra.

Pomůcky, hardware, software

• Žák/yně: PC nebo tablet s připojením na internet
• Učitel/ka: PC s připojením na internet, dataprojektor

Zdroje

GeoGebra - matematické aplikace. GeoGebra Klasik

Potřebné vstupní znalosti a dovednosti

• Oborové
  • přehled o různých typech trojúhelníků podle velikosti vnitřních úhlů nebo podle délek stran
  • zběhlost v určování polohových vztahů dvou různých přímek v rovině
  • znalost vět o shodnosti a podobnosti trojúhelníků
  • schopnost určit poměr podobnosti trojúhelníků
  • porozumění pojmům obvod a obsah trojúhelníku
• Digitální
  • ovládání základních geometrických nástrojů programu GeoGebra (Mnohoúhelník, Střed, Úsečka, Vztah mezi objekty)

Přínos využití digitálních technologií

Žák/žákyně používá počítačové dynamické modelování k objevení vlastností středních příček trojúhelníku a využívá efektivní metrické nástroje programu k ověření vlastních hypotéz.

Metodická poznámka

Doporučujeme na začátku hodiny se žáky zopakovat a na tabuli stručně zapsat věty o shodnosti a podobnosti trojúhelníků.

V úloze 1 uvažujeme trojúhelník ABC jako vzor, trojúhelník DBE jako jeho obraz.

Program stanoví v našem případě obvod nebo obsah útvaru sestrojeného pouze pomocí nástroje Mnohoúhelník. Obvod mnohoúhelníku v programu GeoGebra zjistíme výběrem nástroje Vzdálenost a kliknutím na sestrojený mnohoúhelník. Jeho obsah se po konstrukci automaticky zobrazí v algebraickém okně, případně lze využít metrický nástroj Obsah.

Je možné se žáky trénovat různé způsoby formulací vztahů mezi obvody (obsahy) vybraných trojúhelníků v úloze 2 (například dvakrát menší, o 75 % menší apod.).

Na závěr hodiny společně shrneme základní vlastnosti středních příček daného trojúhelníku a provedeme zápis do sešitu.

Popis vzdělávací aktivity

Motivace

V projektové dokumentaci stavby je zakreslen nosník sedlové střechy. V nárysu má sedlová střecha podobu neúplného trojúhelníku a významnou součást nosníku na obrázku 1 znázorňuje vodorovná úsečka, která prochází středy dvou sousedních stran.

Zamyslete se: proč se používá nosník, k čemu slouží?

Řešení

Nosník je stavební prvek, který napomáhá rovnoměrnému rozložení hmotnosti, brání deformaci, zvyšuje pevnost a stabilitu objektu.

Úloha 1 – Konstrukce střední příčky trojúhelníku a její polohová vlastnost

1. Užitím nástroje Mnohoúhelník sestrojte v nákresně programu GeoGebra libovolný trojúhelník ABC.
2. Sestrojte spojnici středů stran AB a BC, využijte nástroje Střed, Úsečka. Spojnici středů dvou stran budeme dále nazývat střední příčka.
3. Přemístěním vrcholů trojúhelníku vytvořte různé typy trojúhelníků, zkoumejte polohu střední příčky a té strany trojúhelníku, jejíž střed nespojuje.
4. Svoji hypotézu ověřte užitím nástroje Vztah mezi objekty.
5. Zdá se, že trojúhelník DBE je podobný trojúhelníku ABC. Dokažte.
6. Jaký je poměr podobnosti a co z toho vyplývá pro délku úsečky DE?
   
   

Řešení

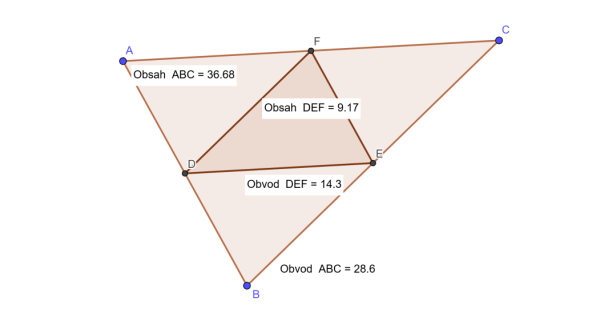
Popsaá střední příčka je v obrázku 2 označena\[ f=DE \]. Program zobrazí informaci o rovnoběžnosti úseček \[ f, b \] a také o jejich různých délkách (obr. 2, pro jeho zvětšení na obrázek klikneme).

Podobnost prokážeme například podle věty uu nebo sus. Platí \[ \frac{|DE|}{|AC|}=\frac{1}{2} \]. Střední příčka má poloviční délku než strana trojúhelníku, jejíž střed nespojuje.

Úloha 2 – Všechny střední příčky v trojúhelníku

Kolik existuje středních příček v jednom trojúhelníku? Mají všechny tyto úsečky uvedené vlastnosti?

1. Sestrojte v trojúhelníku ABC z předchozí úlohy zbývající střední příčky a posuďte, zda každá má výše uvedenou vlastnost.
2. V nákresně vznikl zajímavý obrazec. Kolik vidíte trojúhelníků?
3. Zdá se, že 4 z nich jsou shodné. Vyberte si dva z těchto trojúhelníků a jejich shodnost dokažte.
4. Pomocí nástroje Mnohoúhelník překreslete trojúhelník DEF. Jaký je vztah mezi obvodem trojúhelníku DEF a obvodem trojúhelníku ABC? Ověřte pomocí metrického nástroje Vzdálenost.
5. Jaký je vztah mezi obsahy obou zmíněných trojúhelníků? Ověřte pomocí nástroje Obsah.
   
   

Řešení

1. Každý trojúhelník má tři střední příčky. Každá je rovnoběžná s tou stranou trojúhelníku, jejíž střed nespojuje, a každá má poloviční délku než tato strana.
2. Po sestrojení všech středních příček vidíme celkem 5 trojúhelníků, obr. 3.
   
   

   

3. Například trojúhelník DEF je shodný s trojúhelníkem FAD podle věty sss nebo sus.
4. Obvod velkého trojúhelníku je dvakrát větší než obvod malého trojúhelníku.
5. Obsah malého trojúhelníku je čtvrtinou obsahu velkého trojúhelníku.