Inverzní funkce

Základní informace

• Stupeň vzdělávání: gymnázium, střední škola
• Věková skupina: 16–17 let
• Vzdělávací obor: matematika a její aplikace
• Tematický okruh: závislost a funkční vztahy
• Časová dotace:
  • Výuka: 1–2 vyučovací hodiny
  • Příprava: 0 minut

K čemu aktivita směřuje

Na základě přesně zkonstruovaných grafů porozumění pojmu inverzní funkce a objevení souvislostí s vlastnostmi původní funkce; aplikace poznatků při sestrojení grafů funkcí druhá a třetí odmocnina.

Pomůcky, hardware, software

• Učitel/ka: PC s připojením na internet a dataprojektor
• Žák/yně: PC s připojením na internet nebo tablet s nainstalovanou aplikací programu GeoGebra

Zdroje

GeoGebra – matematické aplikace. www.geogebra.org

Potřebné vstupní znalosti a dovednosti

Oborové

• znalost definice funkce reálné proměnné, znalost osové souměrnosti
• znalost grafu lineární, kvadratické funkce, případně funkce třetí mocniny
• schopnost stanovit definiční obor a obor hodnot z grafu funkce
• porozumění pojmu prostá funkce a jeho souvislosti s monotonií funkce v množině

Digitální

• základní ovládání programu GeoGebra (zápis do algebraického okna, změna nastavení vlastností objektu, zobrazení a skrytí objektu, z konstrukčních nástrojů Osová souměrnost)

Přínos využití digitálních technologií

Rychlé, přesné a efektivní sestrojení grafů funkcí a jejich osově souměrných obrazů.

Metodická poznámka

Sestrojit osu prvního a třetího kvadrantu v nákresně programu GeoGebra lze několika způsoby. Můžeme do algebraického okna zapsat přímo předpis této lineární funkce \[ y=x \], nebo využijeme konstrukčního nástroje Osa úhlu (myšleno souřadnicových os), případně sestrojíme přímku procházející dvěma různými body se stejnými x-ovými a y-ovými souřadnicemi.

Po vypracování úlohy 1 by mělo následovat zavedení pojmu inverzní funkce a jejího značení, včetně zápisu do sešitu. Upozorníme žáky, že program označí (pojmenuje) obraz geometrického útvaru  v osové souměrnosti znakem \[ {f}´ \], nikoli \[ {f}^{-1} \] .

V případě, že nemá vyučující možnost realizovat výuku ve dvou navazujících hodinách matematiky u počítače, doporučujeme body 1–5 z úkolu 1 vypracovat se žáky ručně do sešitu, zavést inverzní funkci a její značení, a v další hodině pokračovat bodem 6 v programu GeoGebra.

Cílem druhé úlohy je objevit souvislost mezi vlastností prostá funkce a existencí inverzní funkce k této funkci. Doporučujeme závěr zjištění zapsat do sešitu. (Ke kvadratické funkci neexistuje funkce inverzní. Inverzní funkci definujeme pouze pro funkci prostou.)

Při odvozování předpisu funkce druhá odmocnina (v úkolu 3) nezapomeneme žákům připomenout, že ryze kvadratická rovnice \[ y^2=x \] má v množině reálných čísel dvě řešení. Ale vzhledem k podmínce \[ D({f^{-1}})=H(f)=\langle0;\infty) \] uvažujeme pouze jedno řešení \[ y=\sqrt{x} \] .  Můžeme žákům ukázat také odvození grafu funkce \[ y=-\sqrt{x} \] jako inverzní funkci.

Předpokládáme, že úlohu 4 žáci řeší samostatně.

Následuje shrnutí všech zjištěných poznatků o existenci inverzní funkce k dané funkci.

Se šikovnými žáky a žáky zvyklými pracovat s GeoGebrou zvládneme aktivity v jedné vyučovací hodině.

Popis vzdělávací aktivity

Úloha 1 - Symetrické grafy lineárních funkcí

1. Sestrojte v programu GeoGebra graf funkce\[ f:y=2x+1 \].
2. Sestrojte přímku, která je osou prvního a třetího kvadrantu, styl čáry vyberte čárkovaný.
3. Užitím nástroje Osová souměrnost sestrojte obraz grafu funkce\[ f \]  v osové souměrnosti podle přímky, která je osou prvního a třetího kvadrantu.
4. V algebraickém okně je zapsáno jedno z ekvivalentních vyjádření nové přímky, přímky označené \[ {f}´ \]. Zapište do sešitu vyjádření proměnné \[ x \] z tohoto zápisu a porovnejte s předpisem původní funkce \[ f \]. Co zajímavého pozorujete?
5. Přemýšlejte: Je obrazem funkce \[ f \] (obrázek 1) zase funkce? Mají nějaké vlastnosti společné?
6. Grafy funkcí \[ f \] a \[ {f}´ \]skryjte. Omezíme definiční obor původní funkce. Do vstupního řádku v algebraickém okně zadejte novou funkci s podmínkou. Zapište: \[ Kdyz(-2\leq{x}\leq3,2x+1) \]. Grafem bude úsečka, obrázek 2.
7. Sestrojte obraz úsečky v osové souměrnosti podle osy prvního a třetího kvadrantu. Pro další práci bude vhodné zobrazit v nákresně také hlavní mřížku (pravé tlačítko myši, nabídka Zobrazit mřížku, výběr Hlavní mřížka).
8. Do sešitu zapište definiční obory a obory funkčních hodnot obou funkcí. Co pozorujete?

Řešení

Pro výraznější odlišení jsme označili původní funkci modrou barvu, její obraz červenou barvou. Kliknutím na obrázek jej zvětšíme.

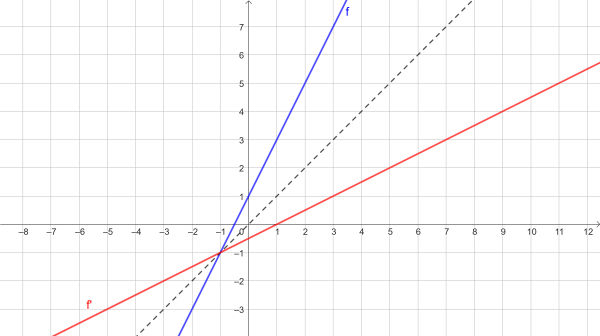
Pro \[ x \] z vyjádření osově souměrné přímky platí \[ x=2y+1 \]. V porovnání s původně zadanou funkcí došlo k záměně proměnných \[ x, y \] .

Obě přímky představují grafy funkcí, obě mají stejný definiční obor i obor hodnot, obě jsou rostoucí.

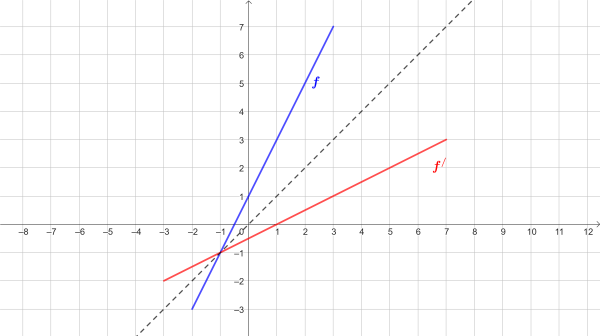
\[ D(f)=\langle-2;3\rangle,H(f)=\langle-3;7\rangle \]

\[ D({f}´)=\langle-3;7\rangle,H({f}´)=\langle-2;3\rangle \]

\[ D({f}´)=H(f),H({f}´)=D(f) \]

Úloha 2 - Symetrický graf kvadratické funkce

1. Pokračujte v otevřeném okně programu GeoGebra. Skryjte zobrazení obou úseček.
2. Do algebraického okna zadejte kvadratickou funkci \[ y=x^2 \] a zobrazte její graf.
3. Zkonstruujte obraz paraboly v osové souměrnosti podle osy prvního a třetího kvadrantu. Zobrazenou křivkou je opět parabola, obrázek 3.
4. Přemýšlejte: Je zobrazená křivka grafem funkce? Zdůvodněte.

Řešení

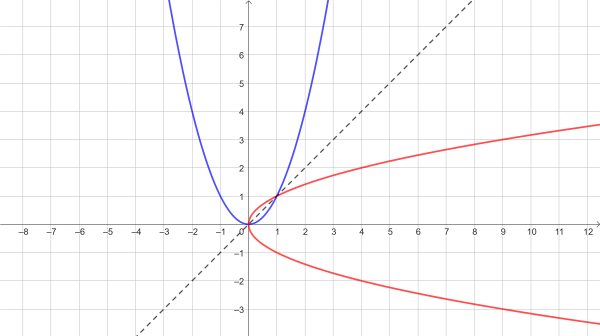
Parabola, která je obrazem kvadratické funkce \[ y=x^2 \] v osové souměrnosti podle osy prvního a třetího kvadrantu není grafem funkce. Nesplňuje základní kritérium, že pro každé \[ x \] existuje právě jedno \[ y \] takové, že \[ y=f(x) \].

Úloha 3 - Inverzní funkce k části kvadratické funkce

1. Skryjte zobrazení obou parabol.
2. Do algebraického okna zapište funkci s podmínkou: \[ Kdyz(x\geq0,x^2) \], v nákresně se zobrazí polovina paraboly.
3. Zobrazte inverzní funkci k zadané funkci s podmínkou (obrázek 4), zapište její obor hodnot.
4. V sešitu odvoďte předpis inverzní funkce k funkci \[ f:y=x^2\land{x}\in\langle0;\infty) \].

Řešení

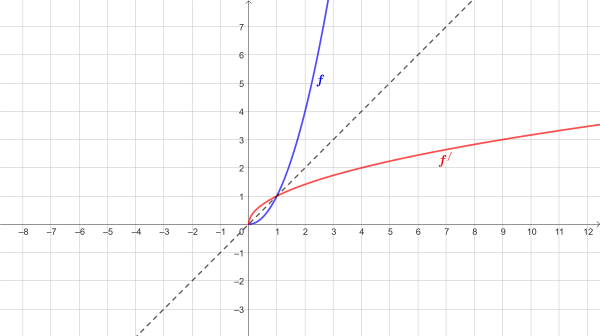
Obor funkčních hodnot funkce \[ f:y=x^2\land{x}\in\langle0;\infty) \] je interval \[ \langle0;\infty) \].

Inverzní funkce má předpis \[ f^{-1}:y=\sqrt{x}~\land{x}\in\langle0;\infty) \].

Úloha 4 - Inverzní funkce k funkci třetí mocnina

1. Skryjte zobrazení obou částí parabol.
2. Sestrojte graf funkce \[ f:y=x^3 \]a určete monotonii funkce.
3. Zobrazte inverzní funkci k funkci třetí mocnina.
4. Najděte předpis této inverzní funkce.

Řešení

Funkce \[ f:y=x^3 \] je na celém svém definičním oboru rostoucí, je prostá, obrázek 5.

Inverzní funkce má předpis\[ f^{-1}:y=\sqrt[3]{x} \].