Hlavním přínosem využití digitálních technologií v této aktivitě je zjednodušení zkoumání a vizualizace matematických konceptů. Rýsování v GeoGebře je rychlejší a díky manipulaci s objekty můžeme zkoumat více modelů pravoúhlých trojúhelníků. Díky digitálním technologiím dochází i ke zjednodušení při měření délek a výpočtů obsahů útvarů.
Aktivita může být využita jako badatelská, kdy žák pracuje samostatně, nebo úlohy provádí současně s učitelem. Výhodná je také půlená hodina, popř. dvouhodinovka. K výukové aktivitě je přiložen pracovní list, který je potřeba vytisknout každému žákovi zvlášť. Pracovní list obsahuje barevný obrázek, můžeme jej však vytisknout i černobíle. Časová dotace závisí na úrovni pokročilosti žáků s danými aplikacemi a také na délce diskusí, které jsou součástí aktivity.
Výuková aktivita se zaměřuje na seznámení se s Pythagorovou větou a následné využití Pythagorovy věty v reálném světě. Aktivitu je vhodné zařadit do výuky matematiky na druhém stupni základní školy po dokončení učiva mocnin a odmocnin. Aktivitu lze rozdělit do dvou hodin – první hodina jako úvod do Pythagorovy věty s první úlohou a druhá hodina zaměřující se na praktické využití Pythagorovy věty (druhá úloha). Vše záleží na zkušenostech a pokročilosti žáků.
Žáci mají k dispozici pracovní list se dvěma úlohami, z nichž v první se pracuje s programem GeoGebra a ve druhé aplikací s Google Maps. Žákům stačí základní znalost obou programů, všechny kroky vedoucí k řešení úloh jsou velmi intuitivní.
První úloha je zaměřena na seznámení se s Pythagorovou větou. Nejdříve mají žáci za úkol sestrojit v GeoGebře pravoúhlý trojúhelník a čtverce sestrojené nad stranami tohoto trojúhelníka dle pokynů v zadání. Výsledek by měl vypadat následovně:
Poté žáci pohybují s trojúhelníkem v souřadnicové soustavě souřadnic a hledají vztahy mezi stranami trojúhelníka a čtverci sestrojenými nad stranami trojúhelníka. V zadání je k dispozici tabulka, do které žáci zapisují hodnoty délek stran a obsahů čtverců ze tří zvolených trojúhelníků, které slouží jako izolované modely. Následovně by měli být schopni vztahy vypozorovat a zapsat svými slovy Pythagorovu větu.
Ukázka možného řešení tabulky:
| \[ a \] | \[ b \] | \[ c \] | \[ a^2 \] | \[ b^2 \] | \[ c^2 \] |
| \[ 1 \] | \[ 2 \] | \[ 2.24 \] | \[ 1 \] | \[ 4 \] | \[ 5 \] |
| \[ 1 \] | \[ 3 \] | \[ 3.16 \] | \[ 1 \] | \[ 9 \] | \[ 10 \] |
| \[ 3 \] | \[ 5 \] | \[ 5.83 \] | \[ 9 \] | \[ 25 \] | \[ 34 \] |
Po seznámení se s Pythagorovou větou následuje aktivita na její využití prostřednictvím práce s mapou v digitální podobě. Žáci se přesouvají do centra španělského města Barcelona, kde mají za úkol zjišťovat vzdálenosti určitých míst, jak pěší, tak přímé. Všechna místa žáci dostanou vyznačená na obrázku mapy v pracovním listě, jejich úkolem je místa na mapě nejdřív najít. Danou situaci namodelují v aplikaci Google Maps a zjistí, kolik metrů má trasa od Sagrada Família na Placa de la Sagrada Família a z tohoto náměstí ke škole Claret School of Barcelona. Díky tomu, že jsou ulice na sebe kolmé a rovnoběžné, jsou schopni pomocí Pythagorovy věty zjistit přímou vzdálenost mezi počátečním a koncovým bodem trasy. Kontrolu výsledku žák provede opět v aplikaci Google Maps, pomocí tlačítka Změřit vzdálenost.
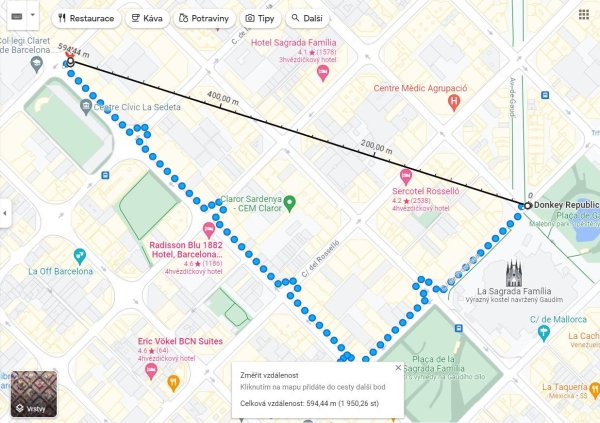
Nedílnou součástí aktivity je i diskuze například o tom, proč se výsledek získaný vlastním výpočtem a výsledek, který jsme získali měřením v aplikaci Google Maps, liší. Žáky můžeme nechat vymýšlet další příklady a reálné situace, kdy se hodí využití Pythagorovy věty. Po celém konci aktivity je žák schopen vyslovit Pythagorovu větu a zároveň ji využít při dopočítání přepony v pravoúhlém trojúhelníku.
Žáky práce s GeoGebrou velmi baví, rychlejší žáci si dokonce zkouší i další techniky (barvy objektů, názvy, písmo…). Ve výuce je potřeba poskytovat individuální pomoc. Při práci s GeoGebrou i s mapou se můžou mezi žáky jevit větší rozdíly v rychlosti práce. Ve chvíli, kdy má žák hotovo, může jít pomáhat spolužákům. Jednotlivé kroky v GeoGebře z první úlohy učitel může sdílet na dataprojektoru.
Slabším žákům může pomoci hledat trojúhelníky s celočíselnými délkami odvěsen. Doporučuji také žáky upozornit na to, že do tabulky některé hodnoty píšeme zaokrouhleně (např. na dvě desetinná místa). Po dokončení první části aktivity by mělo proběhnout společné shrnutí výsledků a kontrola Pythagorovy věty s diskusí (např. Pythagorova věta a tupoúhlý/ostroúhlý trojúhelník). Druhá aktivita je jednodušší, někteří mají práci rychle hotovou, někteří opět potřebují pomoc spolužáků. Žáky vždy baví vymýšlet podobné úlohy, můžeme jim tím zadat menší práci navíc.
Všechny články jsou publikovány pod licencí Creative Commons BY-NC-ND.
Článek nebyl prozatím komentován.
Pro vložení komentáře je nutné se nejprve přihlásit.
Článek není zařazen do žádného seriálu.
