Odchylka tělesové a stěnové úhlopříčky krychle aneb Záleží na úhlu pohledu?

Základní informace

• Stupeň vzdělávání: gymnázium, střední škola
• Věková skupina: 16 - 19 let
• Vzdělávací obor: matematika a její aplikace
• Tematický okruh: geometrie
• Časová dotace:
  • Výuka: 1 vyučovací hodina
  • Příprava: 0 minut

K čemu aktivita směřuje

K sestrojení dynamického 3D modelu užitečného pro vizualizaci problému, k využití nástroje programu na ověření správnosti odhadu velikosti odchylky přímek v prostoru a ke stanovení velikosti úhlu výpočtem.

Pomůcky, hardware, software

• Učitel/ka: počítač s připojením na internet, dataprojektor
• Žák/yně: počítač s připojením na internet, kalkulátor

Zdroje

GeoGebra - matematické aplikace. GeoGebra Klasik

Potřebné vstupní znalosti a dovednosti

• Oborové:
  • znalost pojmů tělesová a stěnová úhlopříčka krychle, odchylka různoběžných přímek;
  • porozumění polohovým vztahům přímek a rovin v prostoru;
  • schopnost vymezit jednoduchý řez krychle danou rovinou;
  • způsobilost orientovat se v rovnoběžném zobrazení krychle;
  • znalost goniometrických funkcí definovaných v pravoúhlém trojúhelníku.
• Digitální:
  • zkušenosti s prací v programu GeoGebra (nastavení 3D prostředí v GeoGebra Klasik nebo přímo využití 3D prostředí);
  • základní obeznámení se zobrazením 3D prostředí programu GeoGebra (3D nákresna, algebraické okno, ovládání pohybu 3D objektu, ikona Standardní náhled).

Přínos využití digitálních technologií

Efektivní vytvoření dynamického 3D modelu krychle a její tělesové a stěnové úhlopříčky poskytuje názornou vizualizaci polohových i metrických vztahů geometrických objektů v trojrozměrném prostoru.

Metodická poznámka

Doporučujeme, aby si na začátku všichni žáci v obecném Nastavení z nabídky Popisovat vybrali Pouze nové body. V nákresně se tak nebudou zobrazovat zbytečná označení dalších objektů, například úseček.

Po konstrukci modelu krychle žákům zdůrazníme pomalou manipulaci s jejími ovládacími prvky, kterými měníme velikost a rotaci. Seznámíme žáky s funkcí ikony "domů" (Standardní náhled), s jejíž pomocí se vždy můžeme vrátit k původnímu zobrazení tělesa.

Pár minut můžeme se žáky trénovat zobrazení krychle v různých polohách – nadhledy, podhledy apod. Měli by se naučit vnímat znázornění 3D prostoru podpořeného správným značením viditelnosti hran.

První úloha je zaměřena na jednoduché ovládání nástrojů 3D prostředí programu a seznámení se s dynamickou 3D vizualizací krychle.

Ve druhé úloze žáci sestrojí tělesovou a stěnovou úhlopříčku vycházející z jednoho vrcholu krychle a z různých pohledů zkoumají, jak velký úhel by mohly tyto úhlopříčky svírat. Svůj odhad porovnají s hodnotou, kterou jim ukáže měřící nástroj programu.

V tuto chvíli je vhodné začít se žáky diskutovat, jak by se dal úhel vypočítat. Cílem je myšlenka vytvoření řezu roviny (učené různoběžkami) a krychle. Jaký geometrický úvar bude řezem?

Ve třetí úloze žáci zkonstruují řez tělesa touto rovinou, přesvědčí se a zdůvodní, proč jím je obdélník.

V samém závěru žáci provedou na základě známé hodnoty délky hrany krychle (buď obecně nebo konkrétně se zadanou číselnou hodnotou) výpočet velikosti úhlu. V případě, že nechceme, aby děti počítaly obecně, doporučujeme zadat několika skupinkám odlišný rozměr krychle, aby žáci porovnáním ověřili, že na konkrétní délce krychle velikost odchylky stěnové a tělesové úhlopříčky (vycházejících z jednoho vrcholu) nezávisí.

Popis vzdělávací aktivity

Úloha 1 - Konstrukce 3D modelu krychle

1. Sestrojte v grafickém 3D náhledu programu GeoGebra krychli.
2. V nastavení změňte barvu tělesa na černou a nastavte průhlednost na hodnotu blízkou nule (pozor, pokud nastavíte hodnotu nula, zablokujete dynamickou změnu znázornění správné viditelnosti hran).
3. Pomocí aktivního ukazovátka a různě umístěného kurzoru (v manipulačních bodech – na obrázku 1 označeny B a C - a mimo zmíněné body) pomalým tažením měňte polohu a velikost krychle. Popište, jak se mění poloha či velikost krychle.
4. Přes pravé tlačítko myši nejdříve skryjte zobrazení os a roviny. Pak změňte polohu krychle tak, aby se její horní stěna zobrazila do podstavné stěny (ABCD). Co je v tomto případě průmětem krychle?

Řešení

1. Ke konstrukci krychle využijeme počátek soustavy souřadné (na obrázku 1 označen jako bod A) a další bod na ose \[ x \] (bod B). První zobrazená krychle je zbarvena růžově.
2. Po změně barvy a vhodném nastavení neprůhlednosti získáme stejné zobrazení tělesa jako na obrázku 1.

   

3. Bodem B lze pohybovat pouze po ose \[ x \], nastavujeme tak délku hrany krychle. Pomocí bodu C otáčíme krychli podle osy \[ x \]. Těmto bodům říkáme manipulační body a jsou automaticky podbarveny modře. Tažením kurzoru umístěného mimo uvedené body měníme polohu celé podstavné (základní) roviny. Velikost krychle můžeme měnit také rolovacím kolečkem myši.
4. Průmětem krychle je čtverec (obrázek 2).

   

Úloha 2 - Zobrazení úhlopříček

1. Nastavte polohu zobrazení krychle v levém nadhledu.
2. Sestrojte úsečky EC a HC. Jak tyto úsečky v tělese nazýváme? Odhadněte a zdůvodněte, jak velký úhel spolu tyto dvě různoběžky svírají.
3. Pomocí měřicího nástroje Úhel programu zjistěte skutečnou velikost tohoto úhlu.

Řešení

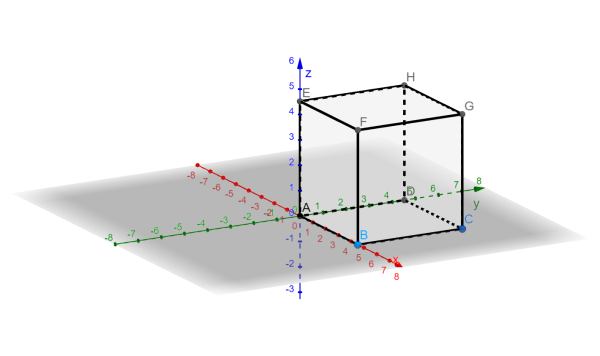
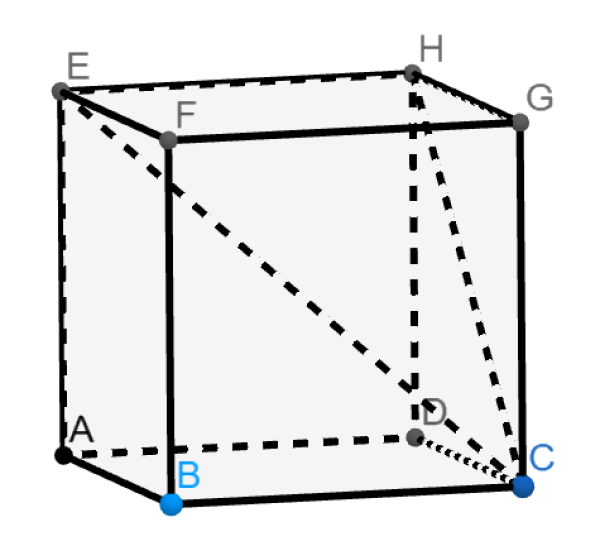
Zkoumanými různoběžkami jsou tělesová a stěnová úhlopříčka krychle vycházející z vrcholu C, obrázek 3.

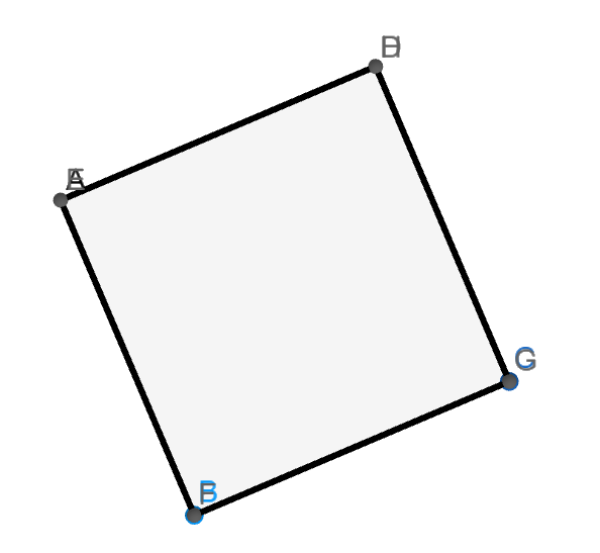
Očekáváme, že žáci budou nejdříve krychlí různě otáčet, aby co nejlépe odhadli velikost požadovaného úhlu. Například při poloze jako na obrázku 4 mohou někteří dospět k úvaze, že zkoumaný úhel má velikost \[ 45° \].

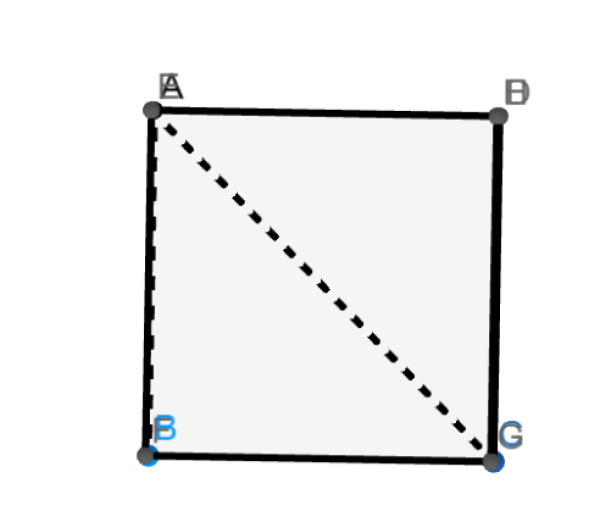
Pro stanovení skutečné velikosti úhlu pomocí nástroje Úhel je potřeba využít jiného vhodnějšího zobrazení krychle než je na obrázku 4. (Vyznačení úhlu lze zvětšit v Nastavení úhlu, na kartě Styl, volba Velikost. ) Zobrazí se výsledek jako na obrázku 5.

Úloha 3 - Ověření správnosti

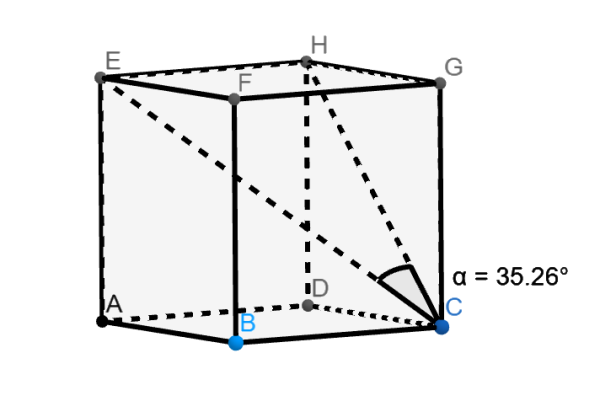
Nejdříve se zaměříme na vyvrácení hypotézy, že zkoumaný úhel má velikost \[ 45° \], a využijeme k tomu nástroje programu.

1. V nastavení vlastností objektu úhel (po kliknutí na pravé tlačítko myši) zrušte zaškrtnutím políčka Zobrazit popis, čímž docílíte skrytí textu s názvem a velikostí úhlu.
2. Dvě různoběžné přímky tvoří jedinou rovinu. Zobrazte ji užitím nástroje Rovina a kliknutím na dvě různoběžky nebo výběrem vrcholů E, C, H krychle. Otáčením měňte polohu zobrazení objektu a ověřte, že zobrazená rovina je ta správná.
3. Sestrojte řez tělesa touto rovinou. Z nabídky nástrojů 3D geometrie vyberte Průnik dvou ploch, klikněte postupně na rovinu a na krychli. Abyste měli jistotu, že neoznačíte pouze část tělesa, doporučujeme kliknout na označení krychle v algebraickém okně. (Další možností je také po kliknutí na rovinu řezu přemístit kurzor na pravděpodobnou část řezu v některé ze stěn.) Zobrazí se řez tělesa rovinou  ECH, obrázek 7.
4. Jaký rovinný útvar je řezem? Může být odchylka úhlopříčky od strany v tomto útvaru \[ 45° \]?
5. Ověřte výpočtem velikost odchylky stěnové a tělesové úhlopříčky krychle. Závisí velikost zkoumaného úhlu na velikosti hrany krychle?

Řešení

Na obrázku 6 je počítačové zobrazení roviny ECH.

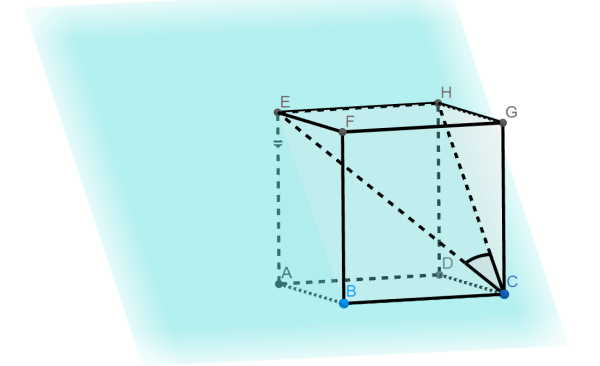
Čtyřúhelník, který je průnikem roviny a krychle, je znázorněn na obrázku 7 červeně.

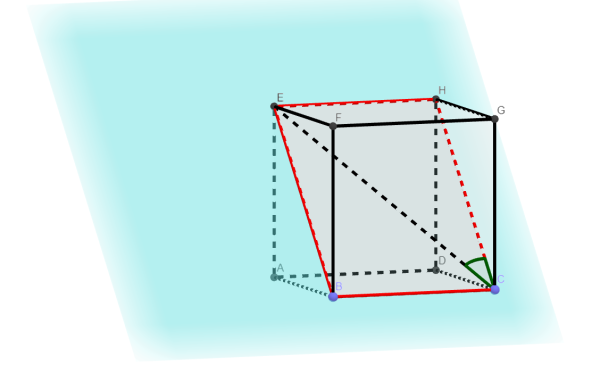
Řezem je v našem případě obdélník. Pravé úhly lze ověřit užitím měřicího nástroje Úhel programu. Že se nejedná o čtyřúhelník se stejnými délkami stran, je zřejmé už ze zobrazeného modelu. Jednu dvojici jeho protilehlých stran tvoří hrany krychle, druhou dvojici stěnové úhlopříčky krychle. Obě tyto informace také využijeme při kontrolním výpočtu. Označíme-li hranu krychle\[ a \], pak úhlopříčka ve čtvercové stěně má v důsledku Pythagorovy věty délku \[ a\sqrt2 \]. Pro výpočet úhlu při vrcholu C v pravoúhlém trojúhelníku CHE využijeme funkci tangens.

\[ \tan\alpha=\frac{a}{a\sqrt2} \], po úpravě \[ \tan\alpha=\frac{\sqrt2}{2} \] a odtud \[ \alpha\doteq35{,}26°\doteq35°16' \]. A to je v souladu s hodnotou, kterou nám poskytl počítačový program.