Jak velký je terezínský bastion?

Základní informace

• Stupeň vzdělávání: gymnázium, střední škola
• Věková skupina: 15–17 let
• Vzdělávací obor: matematika a její aplikace
• Tematický okruh: geometrie
• Časová dotace
  • Výuka: 2 vyučovací hodiny (možno využít 1 hodinu dějepisu)
  • Příprava: 5 minut (stažení obrázku v příloze a uložení do složky dostupné žákům)

K čemu aktivita směřuje

Odhad při porovnání velikosti dvou různých rovinných útvarů a následné experimentální ověření počítačovým modelováním.

Pomůcky, harware, software

Učitel/ka: PC s připojením na internet, dataprojektor

Žák/yně: PC s připojením na internet, kalkulačka

Zdroje

https://www.pevnostterezin.cz/

https://cs.wikipedia.org/wiki/Fotbal

Potřebné vstupní znalosti a dovednosti

• Oborové
  • znalost způsobů výpočtu obsahů mnohoúhelníků
  • zběhlost při aplikaci přímé úměrnosti
  • porozumění obecnějšímu metrickému pojmu jednotka
• Digitální
  • dovednost vložit obrázek do prostředí nákresny programu GeoGebra
  • schopnost ovládat základní konstrukční a měřicí nástroje programu GeoGebra (konstrukce úsečky daného rozměru, nástroje Kolmice, Rovnoběžka, Průsečík, Mnohoúhelník, Vzdálenost, Obsah, …)

Přínos využití digitálních technologií

Efektivní zjištění potřebných informací a dat, tvorba a využití počítačového modelu k jinak neuskutečnitelnému experimentování.

Metodická poznámka

Cílem první hodiny je především seznámení s významem slova bastion v kontextu historie staveb vojenských pevností, vyhledávání potřebných informací v relevantních zdrojích, seznámení se s populárně naučnými webovými stránkami o pevnosti Terezín a následná diskuze. Proto se nabízí možnost využít spolupráce dalšího pedagoga, který by se tématu věnoval například v hodině dějepisu.

Žákům zadáme za domácí úkol zjistit význam slova bastion (ukázalo se, že ne všichni žáci toto slovo znají).

První vyučovací hodinu se žáky zahájíme diskuzí o bastionu a jeho historickém významu. Poté je vhodné převést řeč na vojenské pevnosti v ČR (zda žáci někdy slyšeli o nějaké historické vojenské pevnosti vybudované na našem území).

Zadání úlohy je jasné, vyhradíme asi 15 minut na zjišťování informací o rozměrech hřiště a plného terezínského bastionu. Poté společně diskutujeme, jaké informace žáci dohledali a v jakých zdrojích. Cílíme na využití webové stránky https://www.pevnostterezin.cz/. Domluvíme se, s jakými konkrétními údaji budeme dále pracovat.

Ve druhé vyučovací hodině provádíme vlastní modelování v programu GeoGebra, hodinu uzpůsobíme podle schopnosti žáků samostatně pracovat s tímto programem.

Žáci vloží obrázek bastionu do aplikace GeoGebra Klasik 6. Z důvodu průběžné kontroly a zachování odpovídajícího poměru velikostí obou objektů (mnohoúhelníku a hřiště) obrázek jednotně ukotvíme. Přes pravé tlačítko myši, nástroj Nastavení a zaškrtnutí nabídky Upevnit objekt umístíme modré manipulační body A, B například do mřížových bodů 0 a 10 na ose  (obr. 1).

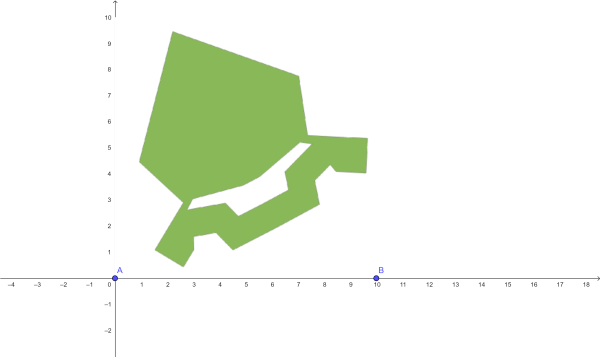
Pokusíme se o odhad. Žáky informujeme, že hřiště budeme umisťovat do „pětiúhelníkové“ horní části bastionu. Ukazuje se problém s výpočtem obsahu pětiúhelníku. Program GeoGebra ale může pomoci. Zjistíme počítačový obsah pětiúhelníku v jednotkách čtverečních. Je zapotřebí výpočtem stanovit kolik metrů ve skutečnosti představuje jedna jednotka v programu GeoGebra. Je důležité si uvědomit, že se snažíme dospět k nějakému „rozumnému“ výsledku, nikoli naprosto přesnému.

Další diskuze se týká postupu řešení zadané úlohy počítačovým modelováním. Žáky vyzýváme k návrhům, přičemž se je snažíme navést na využití nástrojů programu.

Po skončení krátké diskuze se domluvíme na společném postupu: stanovení rozměrů (v jednotkách programu) obdélníku znázorňujícího fotbalové hřiště a jeho konstrukce.

Vlastní konstrukci a přemísťování provádějí žáci samostatně.

V případě, že nám zbude čas, můžeme žáky směrovat návodnými otázkami ke zjištění dalších poznatků o terezínské pevnosti, resp. bastionu. 

Například:

• Měl nějaký význam pětiúhelníkový tvar bastionu?
• Kolik bastionů pevnost má? Kolik různých?
• Stavěla se pevnost jako symetrický útvar? Mělo to svůj důvod?

Popis vzdělávací aktivity

Úloha je zaměřena na porovnání velikosti (ve smyslu obsahu) a tvaru bastionu jakožto stavebního prvku historických vojenských pevností se soudobým fotbalovým hřištěm.

Úloha – Bastion a fotbalové hřiště

Vešlo by se fotbalové hřiště na plochu terezínského plného bastionu? Ověření proveďte pomocí programu GeoGebra a využijte obrázek v příloze.

Řešení

Rozměry fotbalového hřiště nejsou zcela přesně dány, jeho šířka a délka se obvykle pohybuje v určitých rozpětích. Například podle Wikipedie mají profesionální soutěže UEFA pro vybrané kategorie stanoveny rozměry hřiště 105 m x 68 m, patří tak k těm největším. V dalších krocích pracujeme právě s těmito hodnotami.

Informace o rozměrech plného bastionu (obr. 2), který je součástí vnitřního opevnění pevnosti Terezín (a spoustu dalších zajímavostí nejen z historie pevnosti), vyhledáme na populárně naučných webových stránkách https://www.pevnostterezin.cz/. Jejich součástí je také mnoho modelových obrázků. Dozvíme se, že délka líce plného bastionu je 117 m a boky měří 54 m, viz https://www.pevnostterezin.cz/struktura-pevnosti/vnitrni-val/bastion/plne-bastiony/.  

Výpočet začneme hrubým odhadem. Celková plocha fotbalového hřiště výše uvedených rozměrů je 7 140 m². Je zřejmé, že hřiště bychom chtěli umístit do „pětiúhelníkové“ horní části bastionu, kterou považujeme za souměrný útvar. Ke zjištění obsahu pětiúhelníku využijeme možnosti programu GeoGebra. Přiložený obrázek vložíme do nákresny a užitím nástroje Mnohoúhelník zjistíme také hodnotu jeho obsahu v jednotkách čtverečních (zobrazí se jako číselný údaj v algebraickém okně). Řekněme, že obsah pětiúhelníku je 26,61 j² (obr. 3). V nastavení úsečky (označené strany mnohoúhelníku) výběrem zobrazení popisu Název a Hodnota (nebo pomocí nástroje Vzdálenost) stanovíme délku líce nebo boku modelu bastionu. Vybereme si např. líc, v obrázku 3 měří strana \[ \small{f~=~5{,}14 ~\mathrm{j}} \]. Jednoduchým výpočtem užitím přímé úměrnosti zjistíme, kolik metrů ve skutečnosti odpovídá jedné jednotce na počítačovém modelu. Platí \[ \small{1~\mathrm{j}~\doteq~23~\mathrm{m}} \] a \[ \small{1~\mathrm{j^2}~\doteq~529~\mathrm{m^2}} \]. Obsah pětiúhelníkové části plného bastionu pak bude přibližně 12 167 m², což je o mnoho více, než je plocha fotbalového hřiště.

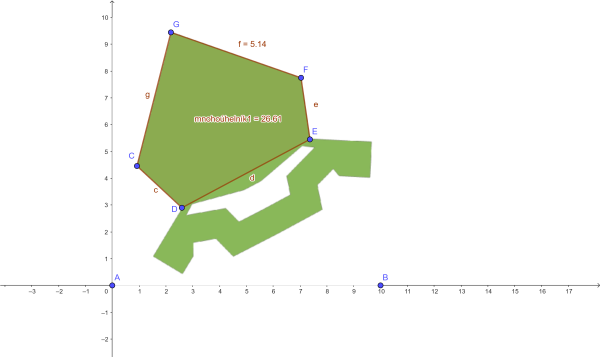
Zdá se, že se fotbalové hřiště na plochu bastionu vejde. Při porovnávání hraje také důležitou roli geometrický tvar každého z objektů. V nákresně programu sestrojíme obdélník o rozměrech odpovídajících přepočtu rozměrů fotbalového hřiště (105 m x 68 m) na jednotky v modelu.

Při hodnotě\[ \small{1~\mathrm{j}~\doteq~23~\mathrm{m}} \] vychází rozměry obdélníku přibližně 4,6 j x 3 j (rozumně zaokrouhlíme), obr. 4.

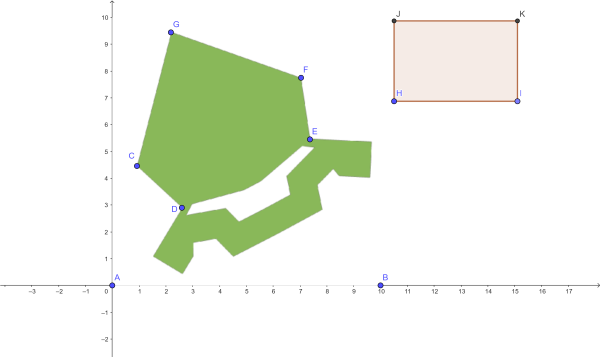
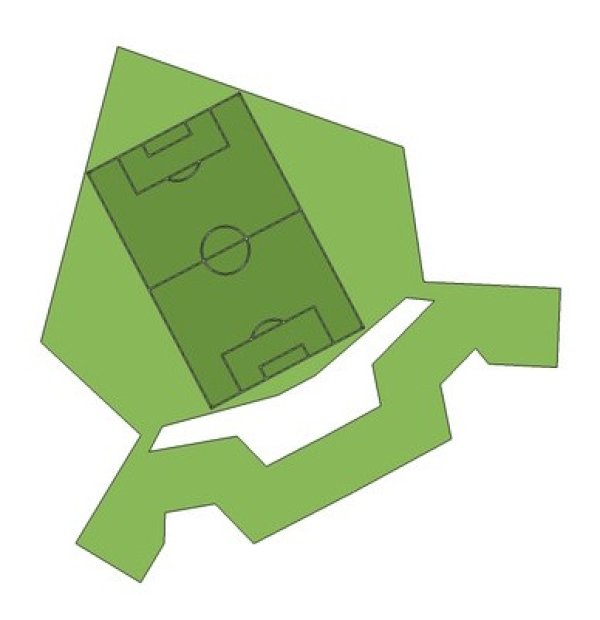
Ke konstrukci obdélníku daných rozměrů využijeme nástroje Úsečka s pevnou délkou, Kolmice, a Kružnice daná středem a poloměrem. Hranici obdélníku překreslíme využitím nástroje Mnohoúhelník a pokusíme se jej umístit do zelené pětiúhelníkové části bastionu tak, abychom ověřili, zda se fotbalové hřiště na jeho plochu vejde, obr. 5. Modře označené body (body H, I) jsou manipulační body, s jejich pomocí je možné otáčet celým mnohoúhelníkem.

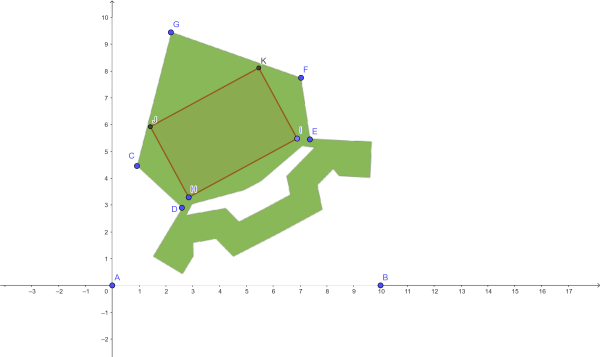
Ověřili jsme, že i největší fotbalové hřiště by pokrylo část plochy jednoho terezínského bastionu a uvědomili jsme si, jak rozměrným objektem je zmíněná část pevnosti.