Učitel: mobilní telefon, tablet nebo počítač připojený k internetu, projektor připojený k počítači / mobilnímu telefonu
Oborové
Digitální
Zdroje
https://activities.graspablemath.com/
Tato aktivita je určena žákům 9. ročníku ZŠ. Žáci budou pracovat ve webové aplikaci Graspable Math. Aplikace Graspable Math je sice v anglickém jazyce, ale její ovládání je velice intuitivní. Základní nastavení aplikace Graspable Math pro výuku matematiky zde. Pokud žáci mají problémy s AJ, lze využít nabídku na hlavním panelu „přeložit stránku jazyka“ a převést text do češtiny. Úkoly lze plnit na počítači, tabletu či mobilním telefonu. Do programu Graspable Math se učitel přihlašuje přes svůj Google účet. Žáci se do aplikace nemusí registrovat, mohou se přihlásit pouze na základě kódu, který učitel vygeneruje (přes nabídku, tj. „Activity bank“, „Create activity“, „Assign to student“) a žákům zašle. Ti jej poté zadají na hlavní stránce aplikace a zvolí nabídku „Whiteboard“ (Obr. 1). Žáci pracují na aktivitě samostatně na svých zařízeních. Na úvod by měl učitel v krátkosti ukázat žákům, jak s aplikací pracovat, což zabere pouze pár minut, jelikož ovládání aplikace je velmi intuitivní. Zdarma lze aplikaci využít pro vytvoření 6 aktivit a pro 12 testování, jinak je aplikace zpoplatněna 5 dolary za měsíc pro účet Premium, kde učitel může vše využívat neomezeně. Webová aplikace obsahuje i velké množství již připravených materiálů do výuky, které lze rovnou použít nebo je podle vlastní potřeby upravovat. Zcela zdarma lze využívat v aplikaci Whiteboards, kde mohou žáci své úkoly také plnit.
Následující aktivita se zaměřuje na téma lineární funkce s využitím aplikace Graspable Math. Žáci si během této aktivity budou ověřovat význam koeficientů a, b u lineární funkce, rozhodovat, zda je funkce rostoucí, nebo klesající, a hledat průsečíky s jednotlivými osami.
Úkoly
a) Jakou společnou vlastnost mají obě zadané funkce související s koeficienty a,b?
b) Určete souřadnice průsečíků funkcí s jednotlivými osami.
c) Rozhodněte, zda jsou funkce rostoucí, nebo klesající.
Řešení úlohy
Ad 1a)
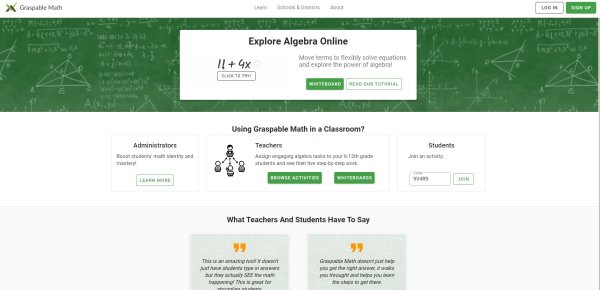
Obr. 1 Aplikace Graspable Math
Přes ikonu insert mohou žáci zadávat matematické výrazy, funkce, texty, YouTube videa, grafy, geometrii (Obr. 2). Program Graspable Math má v sobě naimplementovanou i Geogebru. Pomocí ikony arrange mohou žáci libovolně manipulovat s jednotlivými objekty na pracovní ploše.
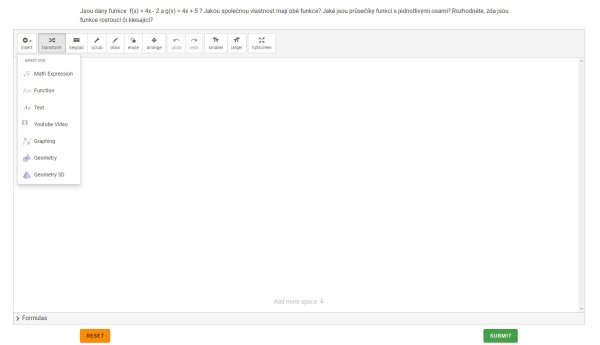
Následně musí žáci zadat na pracovní plochu předpisy funkcí prostřednictvím ikony insert a kliknout na Function a v dolní části se zobrazí klávesnice, pomocí které lze předpis snadno zadat (Obr. 3). S předpisy lze manipulovat pouze po kliknutí na ikonu arrange.
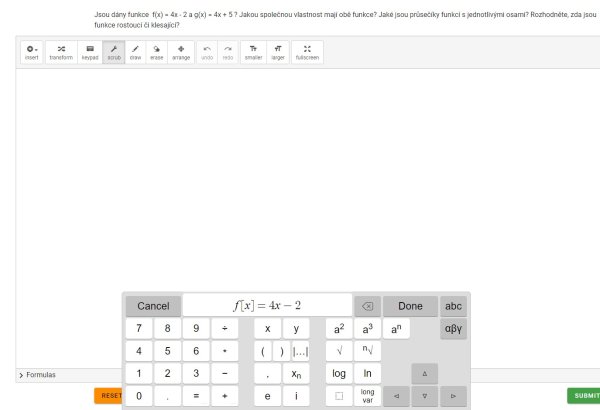
Obr. 3 Zadávání předpisů funkcí
V následujícím kroku žáci vloží prostředí pro tvorbu grafů (insert – Graphing) a zobrazí se prostředí Geogebry (Obr. 4).
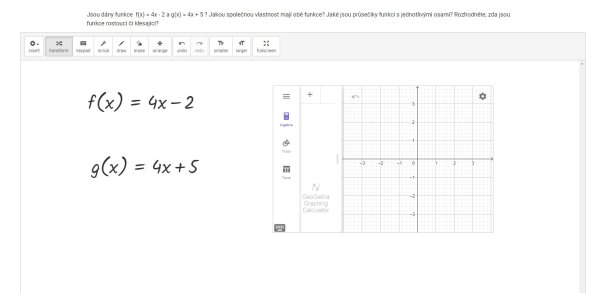
Obr. 4 Vložení prostředí pro tvorbu grafů (Geogebra)
Grafy se v tomto programu vytváří velmi jednoduše, a to tak, že klikneme na ikonu transform a u předpisu se objeví kolečko, na které žáci namíří kurzor. Poté přetáhnou předpis do grafu. Stejný postup zopakují i u druhého předpisu (Obr. 5).
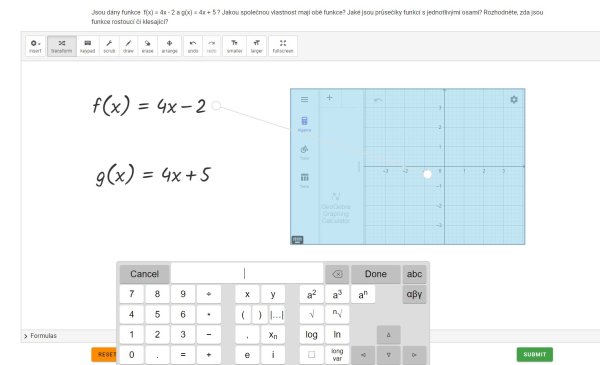
Obr. 5 Vytvoření grafu v Geogebře
Nyní mohou žáci analyzovat obě funkce. Už z předpisu je vidět, že obě lineární funkce mají stejný koeficient a = 4. Z teorie vyplývá, že obě funkce mají kladný koeficient, tudíž obě funkce jsou rostoucí se stejnou směrnicí (se stejným sklonem). Na obrázku je názorně vidět, že pokud mají funkce stejné koeficienty a, jejich grafy jsou navzájem rovnoběžné (Obr. 6).
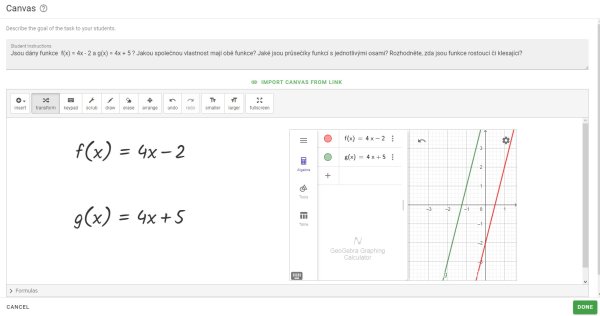
Obr. 6 Grafické řešení úkolu 1a
Ad 1b)
Průsečík grafu s osou x lze zjistit tak, že souřadnice tohoto průsečíku má y-ovou souřadnici nulovou → [?;0]. Početně dosadíme do předpisu funkce za y nulu.
f(x) = 4x – 2 → 0 = 4x – 2 / +2 g(x) = 4x + 5 → 0 = 4x + 5 /-5
2 = 4x / :4 -5 = 4x /:4
0,5 = x ⇒ [0,5;0] -1,25 = x ⇒[-1,25;0]
Průsečík grafu s osou y lze zjistit tak, že souřadnice tohoto průsečíku má x-ovou souřadnici nulovou → [0;?]. Početně dosadíme do předpisu funkce za x nulu.
f(x) = 4x – 2 → y = 4 · 0 – 2 g(x) = 4x + 5 → y = 4 · 0 + 5
y = -2 ⇒ [0;-2] y = 5 ⇒[0;5]
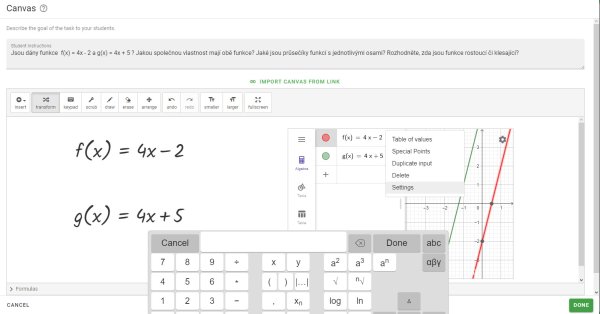
Obr. 7 Průsečíky s osami – nastavení v grafu
Průsečíky grafu s osami nastavíme v aplikaci tak, že u jednotlivých předpisů funkcí v Geogebře klikneme na ikonu tří teček a poté v nabídce klikneme na Special Points (Obr. 7), tím se nám zobrazí průsečíky grafu s jednotlivými osami (Obr. 8). Aby byly viditelné souřadnice bodů, je potřeba potáhnout vodorovnou šipkou pravoúhlou soustavu souřadnic doprava.
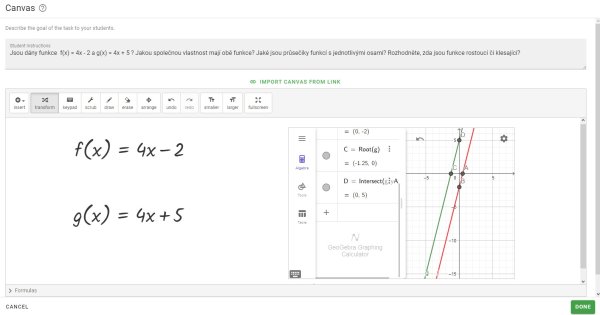
Obr. 8 Grafické řešení úkolu 1b
Ad 1c)
Zda je funkce rostoucí, či klesající, lze zjistit podle koeficientu a.
Pokud je koeficient a > 0 – funkce je rostoucí.
Pokud je koeficient a < 0 – funkce je klesající.
Pokud je koeficient a = 0 – funkce je konstantní.
Vzhledem k tomu, že obě funkce mají koeficient a = 4 ⇒ a > 0 – obě funkce jsou rostoucí.
Úkoly:
a) Jakou společnou vlastnost mají obě zadané funkce související s koeficienty a, b?
b) Jaké jsou průsečíky funkcí s jednotlivými osami?
c) Rozhodněte, zda jsou funkce rostoucí, nebo klesající.
Řešení úlohy
Ad 2a)
V této úloze žáci pracují podobně jako v předchozí úloze. Postup je stejný, liší se pouze předpisy lineárních funkcí (Obr. 9).
Už podle předpisu je vidět, že obě funkce mají společný koeficient b, který je rovný 3. Koeficient b nám vždy naznačí, kde graf protne osu y. Protože mají obě funkce tento koeficient stejný, mají společný průsečík s osou y, který se nachází v bodě [0,3]. Žáci si mohou tuto skutečnost ověřit i výpočtem.
Pokud hledáme průsečík s osou y, musí být x=0, což dosadíme do obou předpisů:
h(x)= 2x +3 → h (x)= 2 · 0 + 3 →h(x) = 3 – průsečík funkce h s osou y je P[0,3].
i (x)= 4x + 3 → i (x) = 4 · 0 + 3 → i (x)= 3 – průsečík funkce i s osou y je P[0,3].

Obr. 9 Grafické řešení úkolu 2a
Ad 2b)
Průsečík grafu s osou x lze zjistit tak, že souřadnice tohoto průsečíku má y-ovou souřadnici nulovou → [?;0]. Početně dosadíme do předpisu funkce za y nulu.
h(x) = 2x + 3 → 0 = 2x + 3 / - 3 i(x) = 4x + 3 → 0 = 4x + 3 /-3
-3 = 2x / :2 -3 = 4x /:4
-1,5 = x ⇒ [-1,5;0] -0,75 = x ⇒ [-0,75;0]
Průsečíky s osou y jsou uvedené v řešení 2a.
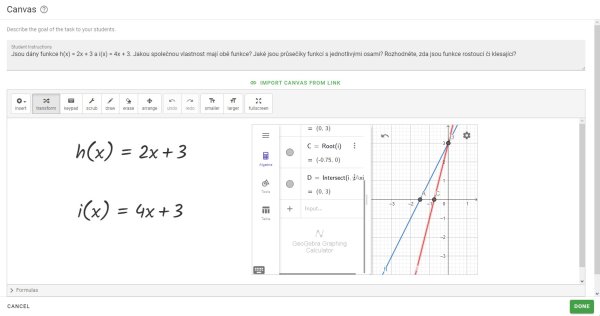
Obr. 10 Průsečíky funkcí s osami
Ad 2c)
Zda je funkce rostoucí, či klesající, lze zjistit podle koeficientu a. Funkce h(x) má koeficient a = 2 a funkce i(x) má koeficient a = 4, tudíž oba koeficienty jsou a > 0, proto jsou obě funkce rostoucí.
V této aktivitě žáci pracují s webovou aplikací Graspable Math, s jejíž pomocí řeší matematickou úlohu zaměřenou na vlastnosti lineární funkce. Žáci v aplikaci zadávají předpisy funkcí, využívají software pro tvorbu grafů, hledají průsečíky funkcí s jednotlivými osami, analyzují vlastnosti lineární funkce, manipulují s jednotlivými prvky.
Doporučení:
Na závěr aktivity mohou žáci zkoumat, jaký vliv může mít změna koeficientů lineární funkce na její průběh. V aplikaci lze tento úkol splnit velmi jednoduše. Žáci budou u funkcí používat tlačítko scrub, pokud na tlačítko kliknou, nad koeficienty lineární funkce se objeví šipky (kterými uživatel musí táhnout směrem nahoru/dolů). Šipkami lze koeficienty zmenšovat/zvětšovat a tím lze i zároveň pozorovat změnu průběhu funkce (Obr. 11 a Obr. 12). Žáci o těchto změnách mohou diskutovat ve dvojicích a společně vyvodí závěry, které následně prezentují spolužákům.
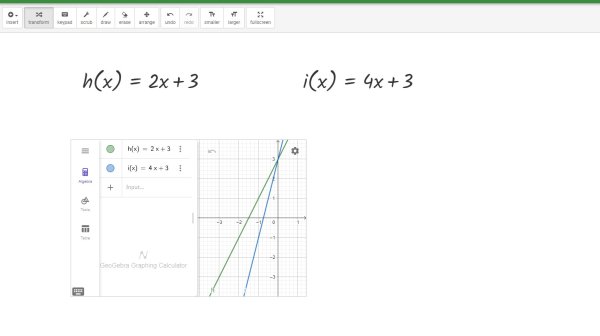
Obr. 11 Průběh zadaných funkcí
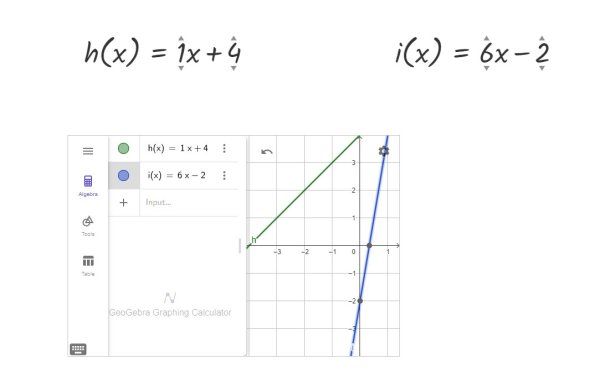
Obr. 12 Průběh upravených funkcí
Ovládání webové aplikace Graspable Math je velmi intuitivní. Žáky bych na úvod seznámila s některými odlišnostmi, které pro práci s aplikací musí znát. V aplikaci se desetinná čísla nezapisují s desetinnou čárkou, ale tečkou, což bývá běžné u aplikací v anglickém jazyce. Dále je potřeba žákům zdůraznit, že označení funkce nemůže být stejné, je třeba f(x), g(x) atd. Často tuto chybu přehlédli, obě funkce si označovali f(x) a při tvorbě grafu se funkce překopírovaly ve stejné zadání. Lze využít nabídku „přeložit stránku jazyka – do češtiny“ na hlavním panelu. Využili ji žáci, kteří mají problémy s AJ, lépe se pak orientují v nabízených možnostech aplikace. Nevýhodou je, že při použití češtiny se při zadávání funkce vkládají do zápisu nesprávné znaky a žáci je musejí přepisovat.
Učitelé mohou tuto aktivitu doplnit i o úkol s funkcí scrub, která umožňuje žákům měnit koeficienty u jednotlivých členů lineární funkce a pozorovat, jak se průběh funkce mění. Ve výuce to žákům přineslo velmi důležité uvědomění toho, jak hodnota konstant ovlivňuje průběh funkce. Při použití funkce scrub je třeba zdůraznit žákům, že je nutné označit konstantu, kterou chceme změnit, a kurzorem táhnout mezi šipkami nahoru nebo dolů podle toho, zda chceme zvětšit, nebo zmenšit konstantu. Nelze jen klikat na šipky!
Článek je publikován pod licencí Creative Commons - Uveďte původ-Neužívejte komerčně-Nezpracovávejte 3.0 ČR .
Článek nebyl prozatím komentován.
Pro vložení komentáře je nutné se nejprve přihlásit.
Článek není zařazen do žádného seriálu.

Národní pedagogický institut České republiky © 2025