Učitel: mobilní telefon, tablet nebo počítač připojený k internetu, projektor připojený k počítači / mobilnímu telefonu
Tato aktivita je určena žákům 8. ročníku ZŠ. Žáci budou pracovat ve webové aplikaci Graspable Math. Aplikace je sice v anglickém jazyce, ale ovládá se velmi intuitivně. Základní nastavení aplikace Graspable Math pro výuku matematiky zde.Pokud by byla pro některé žáky práce v cizím jazyce příliš obtížná, lze využít nabídku na hlavním panelu „přeložit stránku jazyka – do češtiny“. Úkoly je možné plnit na počítači, tabletu či v mobilním telefonu. Do programu Graspable Math se učitel přihlašuje přes svůj Google účet. Žáci se do aplikace nemusí registrovat, přihlašují se pouze na základě kódu zaslaného učitelem (kód učitel vygeneruje přes nabídky – Activity bank – Create activity – Assign to student), který následně zadají na hlavní stránce aplikace a zvolí nabídku „Whiteboards“ (obr. 1). Aplikaci lze propojit též s Google Classroom. Žáci pracují na aktivitě samostatně na svých zařízeních. V úvodu aktivity by měl učitel v krátkosti vysvětlit, jak s aplikací pracovat (nemělo by být potřeba více než pár minut). Zdarma lze aplikaci využít pro vytvoření 6 aktivit a pro 12 testování, neomezený počet úloh je zpoplatněn 5 dolary za měsíc (účet Premium). Webová aplikace obsahuje i velké množství materiálů do výuky, připravených k okamžitému použití nebo libovolné úpravě. Zcela zdarma lze využívat sekci Whiteboards, kde mohou žáci své úkoly také plnit.
Graspable Math nabízí uživateli několik druhů aktivit, s jejichž pomocí si může učivo procvičit. V této aktivitě budou žáci řešit příklady na téma algebraické výrazy. Principem je řešení příkladů přesouváním jejich jednotlivých členů a zadání je plněno v postupných krocích. Aplikace některé kroky nepovoluje, čímž může žákům při řešení příkladů napomoci. Jednotlivé kroky lze vrátit, žáci se tak mohou ve svých výpočtech i opravovat. Navíc získávají ihned zpětnou vazbu o správnosti/nesprávnosti výsledku. Učitel u každého žáka vidí, v kolika krocích příklad vypočítal, kolikrát udělal chybu a příklad resetoval a u jakého cvičení se v okamžiku nachází. K dispozici má rovněž celý postup žákova výpočtu a může mu ihned poskytnout zpětnou vazbu. Doporučuji, aby si učitel nejprve práci s aplikací vyzkoušel, protože správnost výsledku, který se žákům zobrazí např. u algebraických výrazů, závisí na tom, jakou variantu či její ekvivalenci učitel nastaví jako správné řešení. Některá řešení je potřeba rozdělit na dílčí výpočty (např. č. 1b této aktivity), učitel by měl žáky na tento fakt dopředu upozornit. Žáci se mohou setkat i s tím, že přesouváním jednotlivých členů kurzorem lze získat různé ekvivalentní podoby algebraických členů, než na jaké jsou zvyklí. To je velmi užitečné, neboť žáci mívají při počítání s mnohočleny často problém rozpoznat ekvivalentní mnohočleny.
Možné úskalí u vzorců je v tom, že může být pro žáky matoucí to, že pokud žáci potřebují k výpočtu vzorec (a-b)2, který se v nabídce vzorců nenachází, proto je nutné použít vzorec (a+b)2 a aplikace sama rozliší, že uživatel potřebuje vzorec (a-b)2, a proto výraz přepíše v požadovaném tvaru tedy podle vzorce (a-b)2.
Další odlišnost je, že pokud žáci pracují se vzorci a před závorkou se nachází mínus, tudíž se v závorce budou měnit znaménka, aplikace tyto dva kroky udělá najednou jak úpravu podle vzorce, tak i změnu znaménka (Příklad 1b).
Aktivita se zaměřuje na téma algebraické výrazy s využitím aplikace Graspable Math. Žáci si zopakují, procvičí a upevní postupy výpočtů s algebraickými výrazy, konkrétně pravidla pro počítání s výrazy, přednosti u početních operací, úpravy výrazů pomocí algebraických vzorců.
Obr. 1 Prostředí programu Graspable Math
a) 3x · (x - 2) - (1 -6x) (Časová dotace 10 min.)
b) 2m2 - (m + 0,1)2 - (0,2 - m)2 (Časová dotace 15 min.)
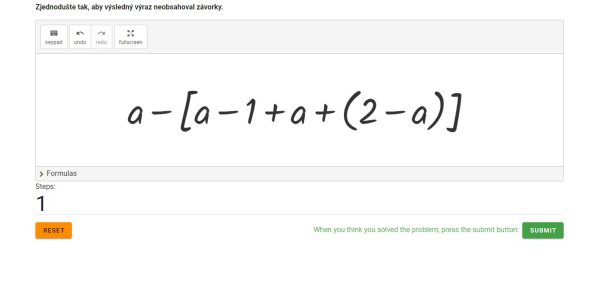
c) a - [a - (1 - a) + (2 - a)] (Časová dotace 10 min.)
Ad 1a)
Žáci řeší algebraické výrazy přesouváním jednotlivých členů. Po zadání kódu se zobrazí zadání příkladu (Obr. 2). Žákům se počítají jednotlivé kroky postupu. Příklad je možné resetovat a začít znovu od začátku.
Obr. 2 Zadání příkladu 1a)
S jednotlivými členy manipulujeme tak, že kurzorem uchytíme člen, který chceme přenášet (pokud se nám uchytí kurzorem pouze část členu, např. v tomto příkladu pouze číslo 3, musíme kurzorem pohnout více dolů a k číslu 3 se připojí i požadovaná proměnná x). Budeme přenášet výraz 3x, kterým potřebujeme v prvním kroku roznásobit závorku 3x· (x - 2), čímž získáme tvar x3x - 6x (Obr. 3). V dalším mezikroku stačí výraz x·3·x upravit, a to tak, že první x kurzorem přeneseme na 3x. Touto úpravou získáme zkrácený tvar 3x2 a následně tvar celého algebraického výrazu 3x2 - 6x - (1 - 6x) (Obr. 4).
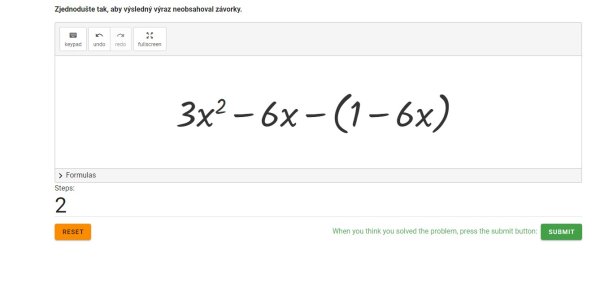
Nyní se musí odstranit závorka - (1 - 6x), a to tak, že znaménko minus přeneseme na závorku a získáme tedy výraz 3x2 - 6x - 1 + 6x (Obr. 5). Nakonec zbývá sečíst výrazy - 6x + 6x (opět přeneseme kurzorem), výsledkem je nula a řešení příkladu je 3x2 –1. Pokud ho máme správně, výsledek se zbarví zeleně (Obr. 6).
Přesouváním jednotlivých členů kurzorem může dojít i ke vzniku různých ekvivalentních podob algebraických členů, např. ekvivalenci u tvaru x23 a 3x2. To, který výsledek, tj. x23 - 1, nebo 3x2 – 1, uzná aplikace za správný (Obr. 7), nastaví učitel při tvorbě této aktivity a nastavování variant řešení. v aplikaci žáci dobře pozorují také komutativnost násobení; tento pojem znají, ale ne každý si ho umí představit nebo vysvětlit na konkrétním příkladu.
Na manipulaci s jednotlivými členy hodně záleží a aplikace umožňuje více způsobů řešení. Pokud uživatel např. poklepe kurzorem na „krát“ před první závorkou, závorka je roznásobena pouze x a v dalším kroku je nutné roznásobit ji ještě číslem 3. V dalším kroku byla závorka odstraněna změnou znamének a následně došlo k odečtení členu 6x. Žáci díky aplikaci nalézají různé možnosti řešení a tím si učivo procvičují (Obr. 8).
Ad 1b)
V tomto příkladu (Obr. 9) se nacházejí dva základní algebraické vzorce, konkrétně druhá mocnina součtu (a + b)2 a druhá mocnina rozdílu (a - b)2. Pro řešení příkladu v tomto programu využijeme ikonu Formulas (vzorce), která se nachází vlevo pod zadáním příkladu. Po rozkliknutí se zobrazí nabídka vzorců. Využijeme vzorec Quadratic Binomial (Obr. 10) a kurzorem přetáhneme vzorec na daný výraz (m + 0.1)2 (Obr. 11).
Tentýž postup zopakujeme i s výrazem (0.2 - m)2. Přestože v nabídce vzorců najdeme pouze výraz (a + b)2, program sám rozezná, že se jedná o podobný výraz lišící se ve znaménku, a vypočítá jej správně. Pro žáky může být matoucí, že zmizely závorky; vzhledem k tomu, že se před závorkou nachází minus a při počítání jsme zvyklí na změnu znaménka v závorce, v aplikaci je tento krok automatický (Obr. 12).
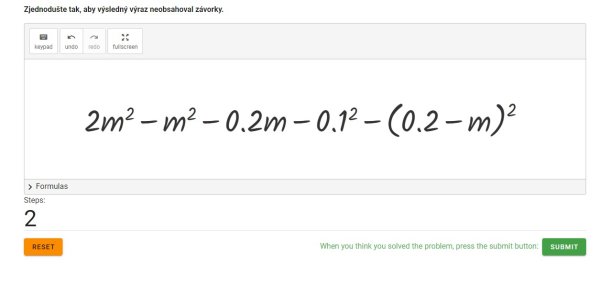
Následně je potřeba prostřední členy obou algebraických výrazů poupravit (vynásobit) a umocnit výraz 0.12 (Obr. 12 – Obr. 15).
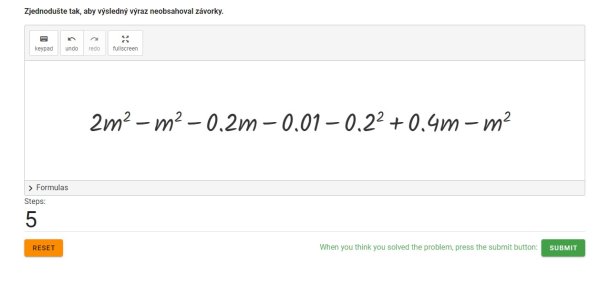
Nyní je potřeba sčítat/odčítat výrazy se stejnou mocninou, případně čísla (Obr. 16 – Obr. 19).
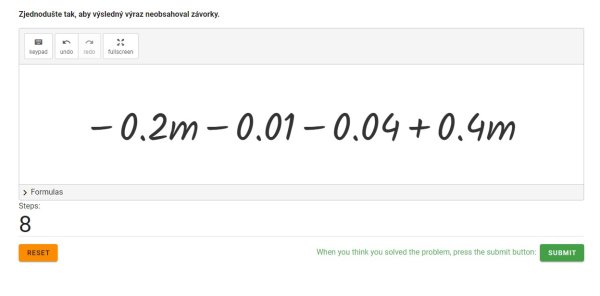
Pokud odstranění závorek pro algebraické vzorce žáky mate, je možné postupovat tak, že žáci řeší nejprve druhou mocninu součtu i rozdílu odděleně a pak získané výrazy dosadí do původní rovnice a pokračují v odstraňování závorek odečtením/sečtením dalších členů (Obr. 20).
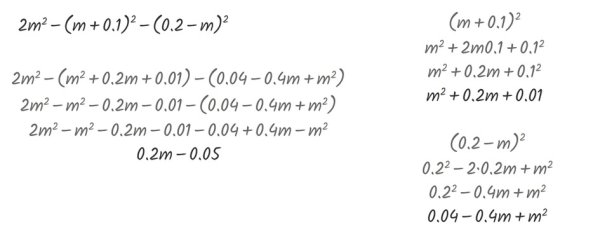
Ad 1c)
V tomto příkladu se nachází dva typy závorek, a to kulatá a hranatá. Nejprve řešíme závorky kulaté a následně hranaté.
Obr. 21 Zadání příkladu 1c)
Nejprve musíme provést odčítání výrazu v hranaté závorce a - (1 - a), kde se změní znaménko. Tím získáme výraz a – 1 + a (Obr. 22). Následně žáci sečtou výraz a + (2a - a); vzhledem k tomu, že se před závorkou nachází +, znaménka se v upraveném výrazu nemění, takže vznikne výraz a - [a - 1 + a + 2a - a] (Obr. 23). Zde aplikace umožňuje ověřit si, že minusem před závorkou dochází ke změně následujících znamének v závorce. To je při výpočtech zásadní krok, jinak nám bude vycházet jiný výsledek. V aplikaci lze chybu rychleji odhalit a opravit.
Sečteme/odečteme všechny členy s proměnnou a v hranaté závorce. Výraz se zjednoduší na tvar a - [a - 1 + 2] (Obr. 24). V hranaté závorce sečteme - 1 + 2 a v hranaté závorce zůstane výraz a + 1 (Obr. 25).
Nyní lze odstranit hranatou závorku, čímž dojde ke změně znaménka u 1 (Obr. 26) a po odečtení a - a žáci získají výsledek -1 (Obr. 27).
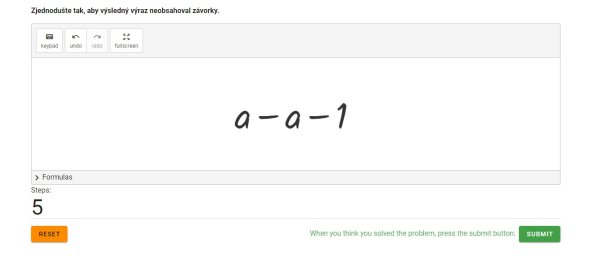
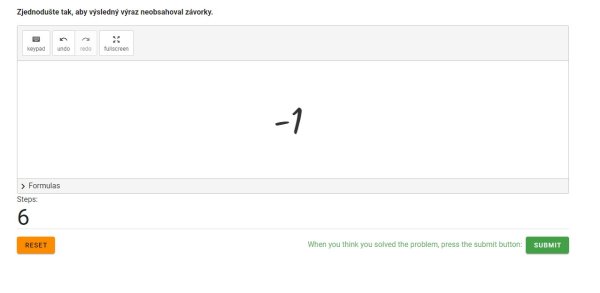
Žáci se opět přesvědčí, že ke správnému výsledku lze dojít různými způsoby řešení. V tomto případě například odstraníme jako první hranatou závorku (Obr. 28). To je možné díky tomu, že v příkladu se nachází pouze početní operace plus a minus, tudíž můžeme odstraňovat závorky zleva doprava.
V této aktivitě žáci řeší příklady na téma algebraických výrazů pomocí aplikace Graspable Math. Aplikace poskytuje okamžitou zpětnou vazbu, zda počítají správně/chybně. Žáci si mohou jednotlivé kroky svého řešení opravit či se k předchozím krokům vracet. Využití digitálních technologií pomáhá efektivně řešit matematické problémy. Žáci řeší i nestandardní situace, se kterými se během klasického počítání na papír nesetkají, a musí na ně reagovat, což přispívá k rozvoji analytického myšlení.
Žáky je třeba v úvodu seznámit s některými odlišnostmi, které pro používání aplikace potřebují znát.
Při řešení příkladu 1b) objevili někteří žáci sami další možnost – kliknutí na exponent druhé mocniny u závorky a rozklad výrazu podle vzorce. Časově je rychlejší, ale chybí možnost rozhodnutí, který vzorec použít, a uvědomění si. Zde někteří žáci i přes upozornění píší desetinnou čárku. Vyžadovala jsem, aby si na chybu přišli sami, popř. si porovnali zadání s jiným spolužákem.
U příkladu 1c) lze využít pro zápis hranatých závorek klávesové zkratky Alt 91 (zleva) a Alt 93 (zprava). Výraz lze upravovat i s kulatými závorkami, vnější závorka je větší. Při přejetí kurzorem u zadání výrazu vpravo nahoře se objeví „kolečko“. Když levým tlačítkem klikneme pod „kolečko“, zobrazí se na dalším řádku upravený výraz. Program provede jen jednu úpravu ve výrazu, např: 2x + x, 3x + 5 + 7, a to vždy u členů nejblíže „kolečku“.
Všechny články jsou publikovány pod licencí Creative Commons BY-NC-ND.
Článek nebyl prozatím komentován.
Pro vložení komentáře je nutné se nejprve přihlásit.
Článek není zařazen do žádného seriálu.
Národní pedagogický institut České republiky © 2025
