Konstrukce trojúhelníků je učivem 7. ročníku ZŠ. Pro konstrukci trojúhelníků využijeme program Robocompass. Pro práci s programem Robocompass je nutné, aby žáci už zvládali rýsovat konstrukce trojúhelníků samostatně. Tato aktivita slouží k opakování učiva konstrukce trojúhelníku pomocí vět sss, sus, usu. Během přípravy na aktivitu doporučuji nejprve žáky seznámit se základními geometrickými pojmy v anglickém jazyce, které jsou v tomto materiálu využity. Sekce How to (Návod – v pravém horním rohu) obsahuje seznam jednotlivých příkazů v anglickém jazyce. Dále doporučuji věnovat se s žáky i procvičování zadávání příkazů, ideální je promítnout program Robocompass např. na interaktivní tabuli. Součástí této aktivity je také interaktivní pracovní list, který slouží jako pomůcka (návod) pro zadávání příkazů, záměrem pracovního listu je i rychlejší pochopení principu zadávání příkazů do programu Robocompass. Program je sice v anglickém jazyce, ale je velmi intuitivní. Úkoly lze plnit na počítači, tabletu či mobilním telefonu. Program je zdarma a není nutné jej stahovat do zařízení, ale pokud žáci nebudou přihlášeni do programu, nemohou svou práci ukládat.
Žáci by si měli před zahájením práce s Robocompassem zafixovat pracovní plochu ve 2D, aby nedocházelo k matení a ztrátě orientace v rovině. Učiní tak kliknutím na ikonu 2D v nabídce vpravo. Žáci nesmí zapomínat, že v některých příkazech se jednotlivé parametry oddělují čárkou, proto se v tomto programu desetinná čárka zapisuje tečkou.
Z kartézské soustavy souřadnic je zjevné, že velikost jednoho čtverečku je 1 x 1 jednotka, podle které se žáci budou v programu Robocompass orientovat.
U každého příkazu lze měnit barvy nebo polohu označení. Setting (nastavení) nalezneme u každého příkazového řádku pod ikonou ozubeného kolečka (Obr. 2). Ke každému příkazu lze přidat i popis, který se potom objevuje při přehrání tohoto kroku v horní liště.
Tato aktivita obsahuje tři úlohy týkající se konstrukce trojúhelníků podle vět sss,sus, usu. Zadání jednotlivých úloh žáci obdrží ve formě interaktivního pracovního listu, který je součástí přílohy. Učitel může pracovní list žákům vytisknout a následně rozdat nebo pracovní list může žákům zaslat do jejich digitálních zařízení, kde jej doplňují.
Aktivitu je vhodné rozdělit do dvou vyučovacích hodin. V první vyučovací hodině doporučuji žáky seznámit s programem Robocompass a jeho fungováním prostřednictvím práce se sekcí How to (návod) a dále doporučuji věnovat se v první hodině principu zadávání příkazů. V druhé části první hodiny učitel zašle/rozdá žákům pracovní list. Žáci ve dvojicích pracují současně s pracovním listem a programem Robocompass. Zbylé úlohy dokončí v následující vyučovací hodině, kde bude poté prostor pro diskuzi ohledně jiných možných způsobů konstrukce trojúhelníků.
Jednotlivé kroky konstrukcí žáci popisují v programu Robocompass prostřednictvím ikony Setting. Na konci aktivity shrnou vlastní postupy řešení u jednotlivých úloh, diskutují o nich a porovnávají rýsování konstrukcí trojúhelníků do sešitu a konstruování v programu Robocompass.
Navštívíme stránky www.robocompass.com, kde se seznámíme se základním ovládáním tohoto programu (Obr. 1). Prostřednictvím pracovního listu, který je součástí této aktivity, si žáci jednotlivé pojmy a princip zadávání příkazů procvičí.
Obr. 1 Prostředí programu Robocompass
V této aktivitě budeme prostřednictvím programu Robocompass zakreslovat geometrické konstrukce pomocí zadávání jednoduchých příkazů. V sekci How to (Návod – v pravém horním rohu) najdeme seznam jednotlivých příkazů v anglickém jazyce.
Žáci si musí nejprve správně nastavit pracovní plochu v programu, a to tím, že kliknou vpravo na ikonu 2D. Tím se jim pracovní plocha zafixuje a nelze s ní dále různě manipulovat. Pokud by si žáci chtěli později prohlédnout svou konstrukci z více úhlů, stačí opět kliknout na ikonu 2D a s plochou je možné znovu manipulovat.
V prvním kroku je potřeba zadat body A a B. Body se v tomto programu zadávají na základě příkazu point (X, Y), kde se za X a Y volí libovolné souřadnice bodu. Před tuto zkratku se uvádí i označení bodu, např. A=point(5,3) (Obr. 2). Bod B bude zadán podobným způsobem jako bod A, ale žáci nesmí zapomenout, že u bodu B musí zadat souřadnice bodu tak, aby vzdálenost mezi body odpovídala 8 jednotkám, tedy B=point(13,3). Pro jednodušší zadávání souřadnic bodů v souvislosti s délkou úsečky volíme úsečku AB rovnoběžnou s osou x.
Obr. 2 Zadání příkazu pro bod A
Po zadání bodů je potřeba oba body propojit vytvořením úsečky AB (Obr. 3). Úsečku je možné vytvořit obecně příkazem line(Bod1,Bod2), kde za Bod1 a Bod2 zvolíme krajní body úsečky a konkrétně v tomto úkolu: c=line(A,B), kde c je označení úsečky, příkaz line označuje čáru.
Obr. 3 Zadání příkazů pro úsečku AB
Dalším krokem při této konstrukci je oblouk k (Obr. 4). Oblouk k zadáme příkazem k=arc(point(Ax,Ay),r,úhel oblouku od, úhel oblouku do), tento příkaz je už složitější.
Zkratka arc označuje oblouk, následně žáci musí zadat souřadnice bodu, který je středem tohoto oblouku, což jsou v tomto konkrétním případě souřadnice bodu A (5,3), dále uvádíme r, tedy poloměr (zde 5 jednotek, což odpovídá délce strany b), a nakonec uvádíme úhel začátku oblouku a konce oblouku (0,90), což znamená, že počátek oblouku je 0°, poté k 0° přidáme 90° proti směru hodinových ručiček. Pozn. Délku oblouku si žáci mohou volit libovolně, např. pokud by zadali do příkazu k oblouku (20,90), tak oblouk začne na 20° vpravo od písmene A a končit bude na 110° proti směru hodinových ručiček.
Obr. 4 Zadání příkazu pro oblouk k
V dalším kroku zadáme podobný příkaz pro oblouk l, konkrétně tedy l=arc(point(13,3),7,90,90). Následně vznikne průsečík oblouků k a l, čímž vznikne bod C (Obr. 5). Průsečík, tedy bod C, vznikl protnutím (intersect) oblouků k a l. Protnutí oblouků zadáme příkazem C=point(intersect(k,l), kde C označuje název bodu a příkaz intersect označuje průsečík oblouků k a l.
Obr. 5 Zadání příkazu pro průsečík oblouků k a l
Na závěr je nutné zadat příkazy pro úsečky AC a BC, kde postup je obdobný jako u zadání příkazu pro úsečku AB, tedy úsečku AC zadáme b=line(A,C) a úsečku BC zadáme a=line(B,C). Vznikl trojúhelník ABC podle věty sss (Obr. 6).
Obr. 6 Trojúhelník ABC dle věty sss
S pracovní plochou lze točit v programu libovolným směrem, takže je možné si celou konstrukci trojúhelníku detailně prohlédnout ze všech úhlů (Obr. 7), což žákům usnadní orientaci. Můžeme si přehrát buď celý postup konstrukce (zelená ikona play nad příkazovými řádky), nebo jen jednotlivé kroky (ikona play u jednotlivých kroků), takže žáci se ke svému postupu mohou kdykoliv vrátit.
Robocompass umožňuje ukládat práci pomocí ikony Save přímo do účtů na Disku Google (Obr. 7). Uživatelé, kteří nepoužívají Disk Google, mohou svou práci sdílet tak, že na ni uvedou přímý odkaz. Žák tedy sdílí soubory se spolužáky a učitelem.
Obr.7 Ukládání konstrukce v programu Robocompass
V prvním kroku je nutné zadat body A a B (Obr. 8). Postup pro zadání bodů je stejný jako v úkolu č. 1.
Obr. 8 Zadání bodů A a B
Po zadání bodů je potřeba oba body propojit, tzn. vytvořit příkazem úsečku AB (Obr. 9). Úsečku žáci vytvoří příkazem c=line(A,B), kde c je označení úsečky, zkratka line označuje čáru a do závorky se uvádí konkrétní body, které jsou krajními body této úsečky.
Obr. 9 Zadání příkazu pro úsečku AB
V dalším kroku už je postup konstrukce trojúhelníku odlišný od předchozího zadání. Nyní je nutné vytvořit ABX (Obr. 10). Vytvoření úhlu ABX se skládá ze dvou příkazů.
Nejprve vytvoříme příkaz pro úhel takto: X=angle(Bod1,Bod2,úhel). V našem případě se jedná o toto konkrétní zadání X=angle(B,A,-60), kde bod B je vrchol úhlu ABX, proto B zapisujeme do příkazu jako první, následně zapíšeme bod A a uvádíme velikost úhlu dle zadání. V této fázi mohou žáci narazit na dvě řešení úlohy. Záleží na zadání velikosti úhlu, pokud velikost úhlu zadají jako 60°, zobrazí se jim bod X pod osou x, což je také správné řešení.
Druhý příkaz, který vede k sestrojení úhlu ABX, je zadání příkazu pro polopřímku BX neboli stranu a, kterou zadáme takto: a=line(Bx,By,Xx,Xy,délka přímky), kde Bx a By jsou souřadnice bodu B a Xx a Xy jsou souřadnice bodu X. Pro žáky bude komplikované odhadnout je tak, aby polopřímka bodem X procházela. Budou se muset snažit odhadnout souřadnice bodu X. Délku přímky si žáci volí libovolně.
Příkazem findangle(c,a) se v konstrukci zobrazí velikost úhlu. V závorce jsou uvedené přímky c a a, které zadaný úhel svírají (Obr. 10). Tento údaj je důležité v konstrukci zadávat, protože slouží k usnadnění vytvoření úhlu, a to tak, že žáci vidí, jakou mají aktuálně velikost úhlu. Pro žáky bývá tato část úkolu obtížná.
Obr. 10 Zadání příkazu pro ABX
Dalším krokem bude zadání příkazu pro oblouk k (Obr. 11), který opět zadáme příkazem k=arc (Bx,By,r, úhlu oblouku od, úhel oblouku do), kde Bx a By jsou souřadnice bodu B (10,2) a dále kde r je poloměr oblouku, který nám značí i velikost strany a (6 jednotek). Velikost oblouku zadáme (60,90), kde oblouk začne, tedy od 60° vpravo od bodu B, a poté přidáme 90° proti směru hodinových ručiček. Velikost oblouku může být zadána libovolně, ale důležité je, aby se oblouk protnul s polopřímkou BX.
Obr. 11 Vytvoření průsečíku v bodě C
Předposledním krokem konstrukce tohoto trojúhelníka je příkaz pro vznik bodu C, který v tomto případě vznikl protnutím polopřímky BX (strany a) a oblouku k. Příkaz zadáme takto: C=point(intersect(a,k)), což znamená, že bod C vznikl jako průsečík strany a s obloukem k.
Posledním krokem je zadání příkazu pro vznik strany b příkazem b=line(A,C) (Obr. 12). Vznikl trojúhelník ABC podle věty sus.
Obr. 12 Trojúhelník ABC podle věty sus
Dalším možným postupem konstrukce je zjednodušení při zadávání úhlu ?, který lze také zadat příkazem otočení (rotate), a tedy zadání je: a=rotate(line(A,B),-60,point(10,2)), kde line(A,B) je objekt, který otáčíme o určitý úhel, v tomto případě o -60°, a point(10,2) značí, kolem kterého bodu k otáčení dochází. V tomto případě se jedná o bod B, který je možné zadat souřadnicemi nebo i pouze názvem bodu. Pokud žáci uvedou úhel 60°, tak je to také správně, protože tato úloha má dvě řešení. Dále vznikne bod C jako průsečík (intersect) oblouku k a úhlu , tedy B=point(intersect(k,a)) a zbývá pouze dorýsovat stranu b=line(A,C). Velikost úhlu zadáváme příkazem findagle (Obr. 13).
Obr. 13 Sestrojení trojúhelníku podle sus pomocí příkazu rotate
Nejprve je nutné zadat příkazy pro body A a B (Obr. 14). Po zadání bodů je potřeba oba body propojit, tzn. vytvořit příkazem úsečku AB. Úsečku vytvoříme příkazem c=line(A,B), kde c je označení úsečky. Do závorky uvádíme konkrétní body, které mají být krajními body úsečky.
Obr. 14 Zadání příkazu pro úsečku AB
Dále je potřeba vytvořit ABX. Vytvoření úhlu se skládá ze dvou příkazů. Nejprve vytvoříme úhel X=angle(B,A,-63). Dále je nutné definovat polopřímku BX neboli stranu a. POZOR, zde bude pro žáky komplikované odhadnout souřadnice bodu X tak, aby jím polopřímka procházela a=line(12,2,9.55,6.80,7) (Obr. 15).
Obr. 15 Zadání příkazu pro velikost úhlu ABX
Následně je potřeba vytvořit příkazy pro BAY. Vytvoření úhlu BAY se také skládá ze dvou příkazů jako v předchozím kroku, tedy Y=angle(A,B,43). Dále je nutné definovat polopřímku AY neboli stranu b. POZOR, zde bude pro žáky komplikované odhadnout souřadnice bodu Y tak, aby jím polopřímka AY procházela, Zadání polopřímky AY (strany b) obecně zní: b=line(Ax,Ay,Yx,Yy,délka přímky). Konkrétní zadání příkazu je: b=line(3,2,8.3,6.95,6). Posledním krokem je označení vzniku bodu C, který zadáme příkazem C=point(intersect(a,b)) (Obr. 16).
Vznikne trojúhelník ABC podle věty usu.
Obr. 16 Trojúhelník ABC podle věty usu
Dalším možným postupem konstrukce podle usu je zjednodušení při zadávání úhlů α, ?, které lze také zadat příkazem otočení (rotate). Zadání tedy zní: a=rotate(line(A,B),-60,point(12,2)), kde line(A,B) je objekt, který otáčíme o určitý úhel, v tomto případě o -60°, a point(10,2) značí, kolem kterého bodu k otáčení dochází. V tomto případě se jedná o bod B, který lze zadat souřadnicemi nebo i pouze názvem bodu. Pokud žáci uvedou úhel 60°, tak je to také správně, protože tato úloha má dvě řešení. Dále zadáme b=rotate(line(A,B),43,point(3,2)) a vznikne bod C jako průsečík (intersect) stran a, b (Obr. 17).
Obr. 17 Sestrojení trojúhelníku podle usu pomocí příkazu rotate
V úloze č. 1 žáci neměli problém se sestrojením trojúhelníku podle věty sss.
Větší potíže nastaly u úlohy č. 2, kde museli sestrojit úhel, který se skládá z několika kroků v aplikaci Robocompass. Nejvíce problematické pro žáky bylo sestrojení strany a, podle příkazu a=line(Bx,By,Xx,Xy,délka úsečky), která prochází bodem X. Zde musejí žáci odhadovat souřadnice bodu X, museli tedy zkoušet různé souřadnice bodu. V aplikaci jim k usnadnění vytvoření úhlu o velikosti 60° sloužil příkaz findangle, který zobrazuje velikost úhlu, viz Obr. 18.
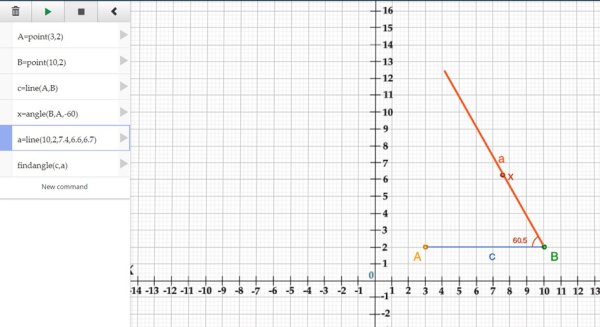
Obr. 18 Nesprávné sestrojení úhlu u trojúhelníku podle věty sus
Další obtíže pro žáky nastaly při příkazu k sestrojení oblouku k=arc (Bx,By,r, úhel oblouku od, úhel oblouku do). V tomto příkazu opět musí žáci zkoušet zadávat velikosti oblouku tak dlouho, dokud se jim oblouk neprotne se stranou a. Na obr. 19 je uvedeno chybné zadání tohoto oblouku. Dalším řešením je využití příkazu rotate jako na Obr. 13.
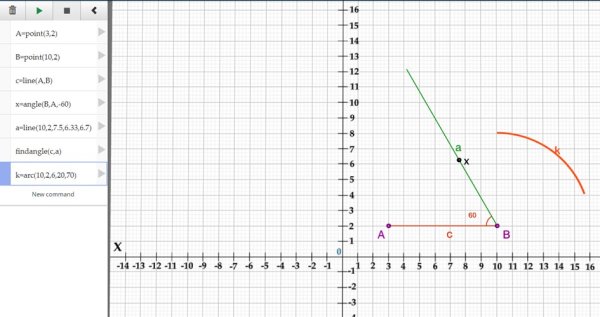
Obr. 19 Chybné sestrojení oblouku u trojúhelníku podle věty sus
Žáci nacházeli i nové alternativy zadávání příkazů, které vedly k úspěšné konstrukci trojúhelníku (Obr. 20). Dvojice žáků nejprve sestrojila oblouk k a až poté sestrojila úhel ABX .
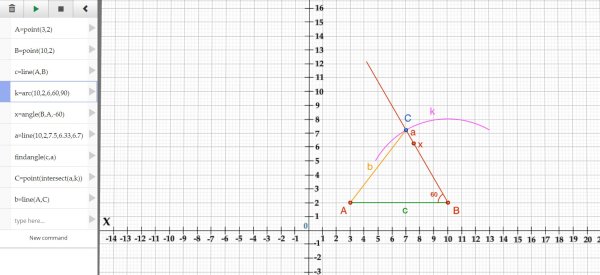
Obr. 20 Jiná varianta zadání příkazů pro sestrojení trojúhelníku podle věty sus
V úloze č. 3 žáci sestrojovali trojúhelník podle věty usu. Ve výuce tato úloha nebyla pro žáky tak náročná jako úloha č. 2. Zde docházelo k chybování pouze ve velikostech úhlů, kde byly chybně zadány souřadnice bodů X a Y. Přímky a, b body X, Y zdánlivě procházely, ale nepřesně, jak je vidět na Obr. 21. Nesprávná velikost úhlů je vidět po zadání příkazu findangle. Zde je také možné sestrojit trojúhelník pomocí příkazu rotate a vyhnout se tak popsaným potížím, viz výše.
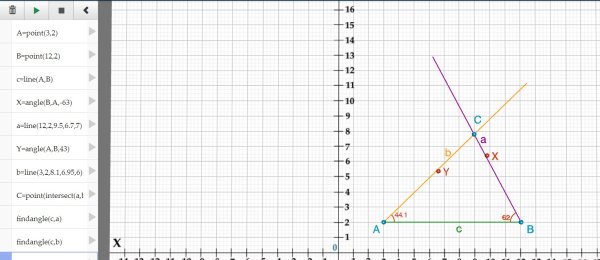
Obr. 21 Chybné zadání velikostí úhlů u trojúhelníku podle věty usu
Doporučuji, aby žáci pracovali s programem ve dvojici, kterou tvoří vždy žák s lepším prospěchem a žák zatížený školním neúspěchem. Tato metoda se mi ve výuce velmi osvědčila, protože žáci spolu ve skupině diskutují a snaží se společně dosáhnout splnění zadaného úkolu. Někteří žáci se ostýchají doptávat se vyučujícího, ale ve skupině se spolužákem s komunikací neměli problém. Další možná alternativa je tandemová výuka spolu s učitelem výpočetní techniky, vzhledem k tomu, že úkoly jsou zaměřené i na algoritmizaci.
Všechny články jsou publikovány pod licencí Creative Commons BY-NC-ND.
Článek nebyl prozatím komentován.
Pro vložení komentáře je nutné se nejprve přihlásit.
Článek není zařazen do žádného seriálu.
