https://support.microsoft.com/
Rychlé a efektivní stanovení počtu dní nebo přesného kalendářního data.
Pokročilí uživatelé tabulkových procesorů využívají funkce s časem (v MS Excel např. DNES(), DAYS(), DENTYDNE(); v LO Calc TODAY() apod.), lze se bez toho obejít.
Pozor, MS Excel začíná od data 1. 1. 1900, LO Calc (analogicky i Tabulky v Google Chrome) od 31. 12. 1899. Číselné hodnoty se sjednotí až od 1. 3. 1900.
Žákům nejdříve zadáme první úlohu (motivační) a společně diskutujeme, jak se k výslednému datu dostaneme a co vše je třeba při jeho stanovení zohlednit. Domluvíme se, že úlohu vyřešíme později.
Vysvětlíme princip práce tabulkového procesoru při počítání s časovými daty. Aby bylo možné v Excelu provádět výpočty s daty, musí dojít k matematickému zobrazení, které konkrétnímu datu přiřadí číslo, a k tomu bylo třeba stanovit počáteční datum. Tím se pro MS Excel stal 1. leden 1900. To znamená, že program chápe datum 1. leden 1900 jako přirozené číslo 1, datum 2. leden 1900 jako číslo 2; číslo 10 odpovídá datu 10. ledna 1900, protože je to v pořadí desátý den po 1. lednu 1900 atd. Zadáme žákům úlohu 2 a za jejich aktivní účasti ji společně řešíme. V případě potřeby žáci použijí kalkulačku a potřebné informace vyhledají v internetových zdrojích.
Ověříme logicky odvozenou číselnou hodnotu v tabulkovém procesoru přes Formát buňky (obecný).
V tuto chvíli je vhodné se vrátit k první, motivační úloze a společně ji se žáky pomocí tabulkového procesoru vyřešit.
Následuje samostatná individuální práce žáků při řešení úlohy č. 4 bez společné kontroly. Cílí na upevnění dovedností práce s formáty časových údajů.
Otázky v úloze č. 5 necháme žáky řešit samostatně, kontrolu výsledků provádíme společně, případně si žáci informaci ověří v internetových zdrojích. Základem úspěšného vyřešení úloh je použití správného formátu časového údaje (obecný, datum krátké, datum dlouhé).
Řešení úloh je popsáno pro užití MS Excel.
Pacient si přinesl domů zásobu léků, které pravidelně užívá jednou denně. K dnešnímu dni má šest balení po 28 kusech tobolek. Rád by si do diáře poznamenal, kdy bude třeba požádat svého lékaře o další. Určete datum aplikace poslední tobolky.
Do buňky zapíšeme dnešní datum, převedeme na obecný číselný formát a doplníme výpočet s využitím odkazu na buňku, ve které je obecný formát dnešního data. Nakonec výsledné číslo převedeme na datum, obr. 1.
Uvažujme, že rozdíl mezi 1. lednem 2023 a 1. lednem 1900 je 123 let, počítáme-li na jeden rok 365 dní, pak nám vychází číslo 44 895. Ovšem nevzali jsme v úvahu přestupné roky. Podle nejrozšířenějšího gregoriánského kalendáře je přestupný každý čtvrtý rok (rok dělitelný čtyřmi beze zbytku), přičemž roky končící v zápise 00 (dělitelné 100) jsou přestupné pouze v případě splnění dělitelnosti čtyřmi sty. A můžeme pokračovat v odhadu. Z předchozího plyne, že rok 1900 nebyl přestupným rokem, rok 2000 ano. Ale pozor, MS Excel považuje rok 1900 také za přestupný! Snadno určíme, že mezi lety 1900–2020 bylo 30 přestupných let plus jeden rok (1900); to znamená, že k prvnímu odhadovanému číslu musíme připočíst 31 dní navíc, jsme tak u čísla 44 926. Rok 2023 bude proto začínat přirozeným číslem 44 927. A je načase tento údaj zkontrolovat přímo v tabulkovém procesoru.
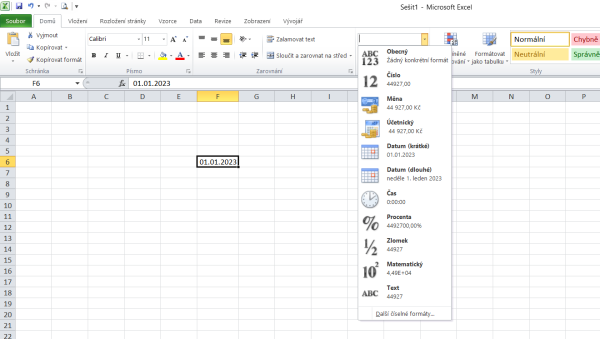
Otevřete MS Excel, do libovolné buňky zapište datum 1. 1. 2023 (možno i bez mezer). Na kartě Domů v nabídce Formát buňky: číslo se zobrazí datum. Rozviňte v tomto okně nabídku dalších číselných formátů a vyberte obecný (obr. 2). Zobrazí se číslo 44 927.
Řešení těchto úloh (vyjma poslední) neuvádíme, odvíjejí se od konkrétního data jejich zadání.
Správný počet zbývajících dní do zahájení LOH si žáci mohou ověřit v internetových zdrojích.
Výroční vysvědčení v uvedený den obdržet nelze, jedná se o neděli.
Výběr číselných formátů je velmi jednoduchý a žákům nečinil žádné potíže. Při společné diskuzi se podařilo přesně odvodit přirozené číslo pro 1. 1. 2023. Přestupné roky si žáci vyhledali. Problémové otázky v úloze č. 5 zvládli vyřešit samostatně. Z důvodu společné kontroly řešení poslední úlohy jsme střídali žáky u učitelského počítače. Je vhodné také vyzvat žáky, aby sami vymýšleli analogické problémové otázky.
Všechny články jsou publikovány pod licencí Creative Commons BY-NC-ND.
Článek nebyl prozatím komentován.
Pro vložení komentáře je nutné se nejprve přihlásit.
Článek není zařazen do žádného seriálu.
