Učí se žáci v našich školách jen pro efekt, výsledky, rodiče nebo také pro sebe, ze zájmu? Umí, co se naučí, použít v životě?
Systémový projekt pro vývoj naší vzdělávací soustavy ve střednědobém horizontu Národní program vzdělávání v České republice (tzv. Bílá kniha, 2001) uvádí: "Úlohou školy bude poskytnout systematickou a vyváženou strukturu základních pojmů a vztahů, které umožní zařazovat informace do smysluplného kontextu vědění i životní praxe… Půjde o novou orientaci vzdělávání: naučit se poznávat - zvládnout metody, jak se učit, jak využívat nové informační a komunikační technologie, jak se vyhnout zahlcení povrchními informacemi, ale naučit se informace zpracovávat, měnit je ve znalosti a aplikovat, umět kriticky myslet a hodnotit…"
Vyučování matematice má v tomto ohledu velice specifické postavení. Svou podstatou je matematika jako vědní disciplína oborem, který je odrazem reálného světa a současně svým teoretickým základem je pro tento reálný svět zdrojem mnoha aplikací. Proto je disciplínou, ve které by měl proces učení probíhat na základě postupného vytváření jednotlivých pojmů a jejich zařazování do poznatkových struktur, ale jistě ne formou předávání hotových poznatků a jejich "bezduchého" algoritmizování.
Vytváření matematických pojmů probíhá v několika etapách, v nichž si žák sám při vyučování vytváří, na základě pozorování a práce s objekty, pozorováním jevů, model skutečnosti. Aby byl tento model správný, je samozřejmě nezbytně nutné, aby jeho konečnou podobu porovnal s představou učitele, realitou, poznatky vědy. Pokud se podaří takový model vytvořit správně, je možné správně pochopit daný pojem i vztahy mezi ním a pojmy dalšími. Pracujeme-li na určitém úkolu v běžném životě, je pro nás jistě velmi důležitá zainteresovanost na nalezení správného řešení - motivace. Po počáteční motivaci si nejprve člověk všímá jevů, ve kterých se nový pojem vyskytuje, a vytváří si tak tzv. separované modely. Dostatečně dlouhým opakovaným pozorováním, manipulací s objekty, představami a získáváním separovaných modelů člověk získá dostatečnou zkušenost s daným pojmem, aby si mohl vytvořit model obecný, univerzální. Bohužel množství potřebných zkušeností pro vytvoření obecného modelu je individuální a nelze je při vyučování jednotně určit. Nedostatečné získání a zpracování separovaných modelů vede k formalismu, tedy k situaci, kdy člověk vytvoří chybný obecný model daného jevu či pojmu. (Hejný, 1989)
Ve školní výuce matematiky však někdy bývá velmi málo času k dostatečně dlouhému manipulování s objekty, čísly, pojmy, a tak velice snadno hrozí formalismus učení. Při vhodném vedení výuky učitelem může například vyučování s podporou počítače přinést žákům během krátkého časového úseku velké množství situací, v nichž si separované modely vytvářejí pozorováním objektů v různých změnách, mohou si sami klást otázky, které vedou k pochopení a vytvoření správné představy o daném pojmu.
Například při výuce osové souměrnosti obrázek, v němž můžeme manipulovat vzorem, osou, přímkou p (na obr. 1) a pozorovat vzájemnou polohu vzoru a obrazu, vysvětlí osovou souměrnost i narýsování osy libovolného úhlu daleko rychleji než rýsování do sešitu, na papír či tabuli. Tím samozřejmě nechceme říci, že by bylo daleko vhodnější místo rýsování jen modelovat s počítačem, určitě ne. Pouze nám některý z matematických programů může usnadnit cestu k vytvoření správného pojmu, který nebude zatížen nemocí formalismu
 |
 |
.


Obr. 1: Osa úhlu
Jedním z doporučení Bílé knihy je …"Vytvořit fond učebnic, počítačových a multimediálních programů a dalších učebních pomůcek, odpovídajících novému pojetí kurikula, který by podporoval, inicioval, koordinoval jejich přípravu a garantoval jejich kvalitu". To znamená promýšlet výuku s pomocí počítače. Ve většině škol probíhá výuka formou instruktivního vyučování (ČŠI, 2005), počítače jsou užívány jen málo a příprava učitelů na takovou výuku a vybavenost škol nejenom co do počtu počítačů, učeben, ale i programů vhodných pro výuku, je nedostatečná.
Již několik let se na Pedagogické fakultě v Českých Budějovicích věnujeme otázce tvorby multimediálních učebních pomůcek a programů pro výuku matematiky na ZŠ. Na toto téma jsou úspěšně řešeny různé granty, rozvíjí se mezinárodní spolupráce a jsou zadávány diplomové práce. Jednou z velice podnětných a zdařilých diplomových prací je práce, v níž se K. Štiková (absolventka studijního oboru Učitelství pro ZŠ, M - Ov) pokusila o jiný pohled na možnost motivace a práce žáků při řešení slovních úloh o pohybu. Připravila program, který umožňuje tvorbu internetových multimediálních aplikací, prezentací a projektů s efektními animacemi.
Slovní úlohy představují pro žáky v mnohých případech nemalý problém právě pro nemožnost aplikace nějakého "jednoduchého" univerzálního algoritmu. Sami učitelé jistě potvrdí, že dobrý a dostatečný výklad může být i pro zkušeného učitele oříškem. Při řešení slovních úloh je problémem jednak porozumění textu, rozbor úlohy, pak i matematizace situace, kterou úloha řeší, a samozřejmě nalezení jejího řešení. Významnou funkci při tom hraje následná zkouška, ověření správnosti, zpětná vazba, která však často bývá jen formální. Při promýšlení didaktických otázek souvisejících s vytvořením malého programu Slovní úlohy o pohybu jsme se zaměřili na otázku motivace, vytváření dostatečného (z hlediska individuálních potřeb) množství separovaných modelů vizualizace a zpětné vazby. Úplnou verzi tohoto programu naleznete (zde). Diplomová práce získala čestné uznání v soutěži SVOČ 2005 v oboru didaktika matematiky na Slovensku.
Po spuštění programu se na první stránce objeví nabídka stručného seznámení s možnostmi, jak lze s programem pracovat při řešení slovních úloh o pohybu. Po volbě Vstupte se otevře další stránka (obr. 2)

 |
Podle textu slovní úlohy se uživatel programu rozhodne, jaký typ situace popisuje jeho zadání a zvolí příslušnou možnost. Tím se dostane na další stránku (obr. 3), velice důležitou z hlediska neformálního pochopení a správného vzniku univerzálního modelu. Zde je nutné dopředu provést odhad o předpokládaném výsledku podle zadání slovní úlohy. Tento odhad se zobrazuje při další práci v horní části obrazovky a je možné jej ještě v průběhu práce změnit. Na konci, po zobrazení konečného výsledku se zobrazený původní nebo opravený odhad řešení úlohy na obrazovce srovná s výsledkem, a je tak možná kvalitní zpětná kontrola a případná korekce špatných úvah, odhadů. Myslíme si, že právě tato část programu je z didaktického hlediska velice přínosná, protože umožňuje pohled na řešenou situaci v několika stadiích pochopení úlohy a přispívá tak ke správnému vytváření představ a pojmů.

 |
Po odhadu výsledku příkladu se dostaneme na další stránku, která je právě onou motivační částí a na které podle individuálních potřeb může každý žák pracovat libovolně dlouho. Po zadání vstupních údajů o délce dráhy a rychlostech tlačítkem Jeď uvede obě autíčka do pohybu z původních (na obr. 4 šedivých) poloh. Může znovu postavit auta na start a pozorovat celou situaci, změnit odhad z předchozí stránky. Při volbě Další stránka (obr. 5) se ještě zlepší možnost vytváření separovaných modelů v mysli žáků. Přibyla tlačítka volby doby jízdy obou aut. Můžeme pozorovat pohyb a vzájemnou polohu aut po 5, 15, 30 a x minutách. Zároveň se nad silnicí na obrázku zobrazuje doba jízdy (v minutách). Stále v levém horním rohu obrazovky vidíme původní odhad a máme možnost "opravy" a tím i zkoušky správnosti řešení zadané slovní úlohy.

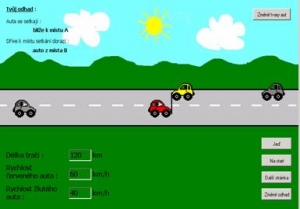 |
| 4. obr |

 |
Důležitá je také možnost řešení zadané úlohy pokusem a odhadem časového intervalu. Zjemňováním a volbou různých časů podle toho, jaký úsek ještě zbývá do setkání obou aut, dochází k dotvoření a upevnění pojmu. Volbou Na další stránku se dostáváme k výsledku (obr. 6) a porovnání nalezeného řešení s původním odhadem. Tlačítkem Zobrazit výsledek se přesvědčíme o správnosti řešení slovní úlohy - uprostřed se zobrazí správný výsledek jako porovnání k odhadu řešení.

 |
| 6. obr. |
Vyzkoušeli jsme práci s programem na několika základních školách a všude jsme se setkali s pozitivním ohlasem jak ze strany žáků, tak vyučujících. Děti uváděly, že porozuměly zadání úlohy a dovedly si ji analyzovat. Další typy zadání(viz obr. 2) už poté nebyly tak neznámé a při řešení se postupovalo rychleji.
Jedním z pozitivních poznatků při práci s programem byla možnost pokusu a omylu. Vědec, matematik, pokud zkoumá nějaký problém, experimentuje při své práci, pozoruje, zkouší donekonečna slepé cesty.
Kutzler (1998) se zamýšlí nad otázkou, jak byly objeveny všechny dosud známé matematické vědomosti a poznatky a jak nalezneme další. Podle jedné z gnozeologicky orientovaných teorií je možné vizualizovat hlavní kroky těchto objevů takto:
Ve fázi experimentování je používán známý algoritmus na vytváření příkladů, pak pozorováním získáme domněnku. Během fáze zpřesňování se domněnka mění pomocí metody důkazu v teorém a algoritmicky použitelná vědomost je pak uvedena jako nový algoritmus. Během fáze aplikace se algoritmus používá na skutečná a fiktivní data. Je možno říci, že řešení skutečných problémů napomáhá zvládnutí nebo usnadnění života, zatímco řešení fiktivních problémů slouží k zábavě a rozptýlení (např. hádanky) nebo k nalezení nových poznatků (např. k uspokojení vědecké zvídavosti).
Proč našim žákům při vyučování tyto způsoby nedovolit? Z nedostatku času? Jsme však sami proti sobě. Pak si můžeme na úvodní otázku tohoto článku odpovědět: Ano, žáci se učí pro efekt, školu, rodiče a výjimečně pro sebe a málokterý poznatek umí použít v běžném životě. Nevidí totiž patřičné souvislosti. Přitom právě například uvedený program pro výuku slovních úloh, nebo jiný způsob použití počítače by mohl někde žádoucím způsobem výuku zkrátit a jinde pak by mohlo zbývat dostatek času na experimentování, objevování, dostatečné zkušenosti se separovanými modely.
Balacheff, N., Kaput, H.: Computer-based learning environments in mathematics. In A. Bishop, J., Clements, K.,Keitel, C., Kilpatrick, J., Laborde, C. (Eds.) International handbook of mathematics education. Dordrecht: Kluwer Academic Publishers, 1996, s.496-501.
Binterová, H., Hošpesová, A.: Objevování v matematickém vyučování podporované Excelem, Univ. S. Boh. Dept. Math. Rep. ser. 10, 2003, s. 267-273, ISSN 1214 - 4681
Výuka funkcí podporovaná počítačem. In: 8. setkání učitelů matematiky všech typů a stupňů škol, Praha: JČMF, 2002, 57-62.
Healy, L., Sutherland, R.: The use of spreadsheets within mathematics classroom. Math. Educ. Sci. Technol. 1990, vol. 21, 6, s. 847-862.
Hejný, M., Kuřina, F.: Dítě, škola, matematika. Konstruktivistické přístupy k vyučování. Praha: Portál, 2001, s. 160-161.
Hejný, M.: Teória vyučovania 2. Bratislava: SPN, 1989.
Hošpesová, A.: What brings use of spreadsheets in the classroom of 11-years olds? In: J. Novotná (Ed.): European Research in Mathematics Education II. Mariánské lázně 24. 2. 2001 - 27. 2. 2001. Proceedings. Praha: Charles University, Faculty of Education, 2002, s. 163-169.
Hošpesová, A.: Are spreadsheets worthwhile for all? In: L. Bazzini, C. W. Inchley: Proceedings CIEAEM 53. Mathematical Literacy in the Digital Era. Ghisetti e Corvii Editori. Multi Media, Milano: 2002, s. 158-164.
Kutzler, B.:. Solving Systems of Equations with the TI-92 (Experimental Learning / Visualization / Scaffolding Method). Hagenberge:bk teachware, 1998, 44 s.
Národní program vzdělávání v ČR (Bílá kniha). Praha: 2001.
Štiková, K.: Návrh pracovních listů pro výuku vybraných typů slovních úloh s podporou počítače. Diplomová práce. 2005.
Výroční zpráva České školní inspekce za školní rok 2003/2004. Praha: ČŠI, 2004.
Vzdělávací program základní škola. Praha: Fortuna, 1996.
Článek je publikován pod licencí Creative Commons - Uveďte původ-Neužívejte komerčně-Nezpracovávejte 3.0 ČR .
Článek nebyl prozatím komentován.
Pro vložení komentáře je nutné se nejprve přihlásit.
Článek není zařazen do žádného seriálu.

Národní pedagogický institut České republiky © 2025